|
Auf dem matheplanet habe ich einen von @Stefan auf die Schnelle gemachten Entwurf für einen Gebietsgraphen gesehen:
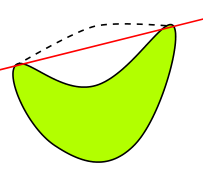
Der Graph illustriert das sogenannte Isoperimetrische Problem, was nach einer Kurve vorgegebener Länge fragt, welche eine maximale Fläche umspannt. Die Lösung ist bekannterweise der Kreis. Das Bild hier zeigt einen ersten Beweisschritt: dass die gesuchte Fläche konvex sein muss, sonst könnte man sie ja durch Spiegeln an der Verbindungsgeraden zweier Randpunkte noch vergrößern bei gleicher Länge, kurz gesagt. Daher soll die rote Gerade das grüne Gebiet eigentlich nur berühren und die gestrichelte Linie soll eine Spiegelung des Gebietsrandes zwischen den Berührungspunkten an der roten Gerade sein. Wie kann man das erreichen? Obiges Bild wurde mit folgendem Code gezeichnet: \documentclass[margin=5mm,tikz]{standalone} \begin{document} \begin{tikzpicture}[scale=0.35] \coordinate (A) at (-4,2); \coordinate (B) at (-2,-2); \coordinate (C) at (2,-2); \coordinate (D) at (4,4); \coordinate (E) at (0,1); \coordinate (F) at (0,4); %Geglättete Polygonzüge \draw[smooth cycle, tension=0.8, thick, fill=green!30!yellow] plot[mark=none, mark size=1.5pt, mark options={fill=red}] coordinates{(A)(B)(C)(D)(E)}; \draw[smooth, dashed, thick] plot[mark=none, mark size=1.5pt, mark options={fill=red}] coordinates{(A)(F)(D)}; %Gerade \draw[thick, red, shorten >=-1cm, shorten <=-1cm] (A)--(D); %%Koordinatensystem %\draw [thick, ->] (-5,0) -- (5,0) node [anchor=north west] {}; %\draw [thick, ->] (0,-5) -- (0,5) node [anchor=south east] {$\mathbf{C}$}; \end{tikzpicture} \end{document} |
|
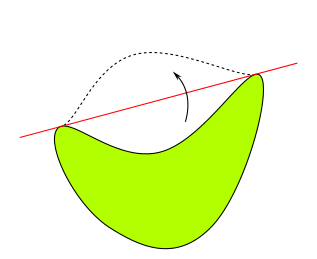
Mir erscheint es durch die Kurvenglättung mittels Aus dem von @Stefan in der Frage ergänzten mathematischen Kontext ergibt sich jedoch, dass es durchaus in Ordnung ist, die Berührungspunkte von Hand anzunähern, da die Verbindungsgerade aus mathematischer Sicht nicht unbedingt genau tangential sein muss.
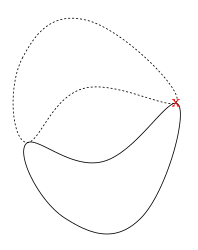
\documentclass[tikz,margin=10mm]{standalone} \usetikzlibrary{calc,arrows.meta} \begin{document} \begin{tikzpicture}[very thick] \tikzset{ form/.pic={ % Koordinaten in Berührungspunkten \coordinate (-O) at (0,0);\coordinate (-A) at (7.87,2.11); % Geglättete Polygonzüge \draw[smooth cycle, tension=0.8,pic actions] plot coordinates{(-.1,-.1)(2,-4)(6,-4)(8,2)(4,-1)}; %\node[red] at (-A){\Huge x}; % zur Kontrolle der Anpassung } } % Gebiet einfügen \pic(Gebiet)[draw,very thick,fill=green!30!yellow]{form}; % Gebiet spiegeln und beschneiden \begin{scope} \clip(Gebiet-O)--(Gebiet-A)--($(Gebiet-O)!0.6!45:(Gebiet-A)$)--cycle; \pic[dashed,very thick,x={(0cm,1cm)},y={(1cm,0cm)},rotate=-60]{form}; \end{scope} % Gerade \draw[red] ($(Gebiet-O)!-.2!(Gebiet-A)$)--($(Gebiet-O)!1.2!(Gebiet-A)$); % Pfeil \draw[-{Stealth[length=4mm,width=2mm]},bend right](5,0.2)to(4.5,2.2); \end{tikzpicture} \end{document} Nötige Zwischenschritte Ermittlung und Kontrolle der Berührungspunkte mit \documentclass[tikz,margin=10mm]{standalone} \usetikzlibrary{calc,arrows.meta} \begin{document} \begin{tikzpicture}[very thick] \tikzset{ form/.pic={ % Koordinaten in Berührungspunkten \coordinate (-O) at (0,0);\coordinate (-A) at (7.87,2.11); % Geglättete Polygonzüge \draw[smooth cycle, tension=0.8,pic actions] plot coordinates{(-.1,-.1)(2,-4)(6,-4)(8,2)(4,-1)}; \node[red] at (-A){\Huge x}; % zur Kontrolle der Anpassung } } \pic(Gebiet)[draw]{form}; \pic[dashed,very thick,x={(0cm,1cm)},y={(1cm,0cm)},rotate=-60]{form}; \end{tikzpicture} \end{document} Die beiden Graphen dürfen sich nicht überschneiden und es darf nur ein „x“ zu sehen sein.
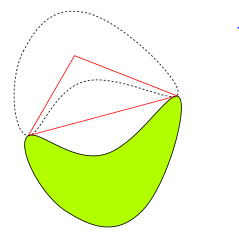
Ermittlung und Kontrolle des Beschneidungsbereiches in dem zunächst
1
Hervorragend gelöst und erklärt! Die Näherung der Randpunkte ist völlig in Ordnung, denn sie sind in mathematischen Kontext beliebig, Hauptsache ihre Verbindungsgerade liegt nicht komplett in der konkaven Kurve. Auch daher habe ich den mathematischen Hintergrund ergänzt. Dass es tangential aussieht, ist eine bildlich schöne Wahl, natürlich. :-) In diesem Sinne kann man den 1. Absatz gern ändern, dass die Wahl per Hand für die Beweisskizze so genug ist.
(28 Mär '14, 12:27)
stefan ♦♦
|

Die Frage ist zum Archivieren gedacht, kein Support benötigt. Antworten sind jedoch sehr willkommen!
@Stefan Vielen Dank für das Einfügen der sehr hilfreichen Erklärung zum mathematischen Hintergrund der Abbildung.