|
Ich plotte manchmal komplexe Funktionen, wo sehr oft Sinus und Kosinus auftauchen. pgfplots erwartet ja Grad als Einheit für das Argument einer trigonometrischen Funktion, ich rechne jedoch eigentlich mit Radiant. Nun kann man einfach mit Ich übersetze mit LuaTeX, da bei hoher Sample-Anzahl wie hier sonst mit pdfLaTeX ein Fehler kommt, kleinere Sample-Zahlen von ca. 40 sind hingegen kein Problem mit pdfLaTeX. \documentclass[border=5pt]{standalone} \usepackage{pgfplots} \pgfplotsset{compat=1.8} \begin{document} \begin{tikzpicture} \begin{axis}[ view = {60}{-60}, hide axis, colormap = {flower}{% color(0cm) = (yellow); color(4cm) = (orange); color(8cm) = (red!40!black); color(12cm) = (red!80!black); color(16cm) = (green); color(20cm) = (green!20!black)}, ] \addplot3[ surf, z buffer = sort, point meta = u, domain = -13.2:13.2, domain y = -37.4:37.4, samples = 80, samples y = 120, variable = \u, variable y = \v ] ( { -u + (2*0.84*cosh(0.4*u)*sinh(0.4*u))/(0.4*((sqrt(0.84)*cosh(0.4*u))^2 + (0.4*sin(deg(sqrt(0.84)*v)))^2)) }, { (2*sqrt(0.84)*cosh(0.4*u)*(-(sqrt(0.84)*sin(deg(v)) * cos(deg(sqrt(0.84)*v))) + cos(deg(v))*sin(deg(sqrt(0.84)*v))))/(0.4 * ((sqrt(0.84)*cosh(0.4*u))^2 + (0.4*sin(deg(sqrt(0.84)*v)))^2)) }, { (2*sqrt(0.84)*cosh(0.4*u)*(-(sqrt(0.84)*cos(deg(v)) * cos(deg(sqrt(0.84)*v))) - sin(deg(v))*sin(deg(sqrt(0.84)*v))))/(0.4 * ((sqrt(0.84)*cosh(0.4*u))^2 + (0.4*sin(deg(sqrt(0.84)*v)))^2)) }); \end{axis} \end{tikzpicture} \end{document}
Kann man durch ein Feature von pgfplots von degree auf radian umstellen? Oder durch eine eigene kleine Reprogrammierung? Wenn das eher ein Feature-Request ist, dann möchte ich meinen Wunsch mit dieser Blume freundlich überreichen. |
|
Innerhalb der naechsten vier Wochen wird die neue Version Diese wird mit global konfigurierbarem Format fuer trigonometrische Funktionen kommen: man schreibt dann Das angefragte Beispiel wuerde damit \documentclass[border=5pt]{standalone} \usepackage{pgfplots} \pgfplotsset{compat=1.8} \pgfplotsset{trig format plots=rad} \begin{document} \begin{tikzpicture} \begin{axis}[ view = {60}{-60}, hide axis, colormap = {flower}{% color(0cm) = (yellow); color(4cm) = (orange); color(8cm) = (red!40!black); color(12cm) = (red!80!black); color(16cm) = (green); color(20cm) = (green!20!black)}, ] \addplot3[ surf, z buffer = sort, point meta = u, domain = -13.2:13.2, domain y = -37.4:37.4, samples = 80, samples y = 120, variable = \u, variable y = \v ] ( { -u + (2*0.84*cosh(0.4*u)*sinh(0.4*u))/(0.4*((sqrt(0.84)*cosh(0.4*u))^2 + (0.4*sin(sqrt(0.84)*v))^2)) }, { (2*sqrt(0.84)*cosh(0.4*u)*(-(sqrt(0.84)*sin(v) * cos(sqrt(0.84)*v)) + cos(v)*sin(sqrt(0.84)*v)))/(0.4 * ((sqrt(0.84)*cosh(0.4*u))^2 + (0.4*sin(sqrt(0.84)*v))^2)) }, { (2*sqrt(0.84)*cosh(0.4*u)*(-(sqrt(0.84)*cos(v) * cos(sqrt(0.84)*v)) - sin(v)*sin(sqrt(0.84)*v)))/(0.4 * ((sqrt(0.84)*cosh(0.4*u))^2 + (0.4*sin(sqrt(0.84)*v))^2)) }); \end{axis} \end{tikzpicture} \end{document}
Vorab Versionen wird es in Kuerze unter http://pgfplots.sourceforge.net/ geben. Zu beachten ist, dass der systemdefault in den folgenden Versionen nicht auf Radians umgestellt wird - das waere doch ein grosser Bruch (selbst mit |
|
Man kann auch den Bereich der Parameter umstellen, z.B. von 0:pi auf 0:180, dann kann man auf Hier ein Beispiel, was komplett in Grad rechnet. Es ist die Oberfläche einer Kugelflächenfunktion, spherical harmonic surface, entsprechend einer Funktion hier, original in Radiant. Wieder mit LuaLaTeX zu übersetzen, weil bei der hohen Anzahl samples pdfLaTeX TeX capacity exceeded kommt. \documentclass[border=5pt]{standalone} \usepackage{pgfplots} \pgfplotsset{compat=1.8} \renewcommand*{\r}{(sin(4*u)^3 + cos(2*u)^3 + sin(6*v)^2 + cos(6*v)^4)} \begin{document} \begin{tikzpicture} \begin{axis}[ view = {120}{310}, hide axis, colormap = {flower}{ color(0cm) = (yellow); color(4cm) = (yellow!70!red); color(8cm) = (red!60!black); color(12cm) = (red!90!black); color(16cm) = (green); color(20cm) = (green!20!black)}, ] \addplot3[ surf, z buffer = sort, point meta = u, domain = 0:180, domain y = 0:360, samples = 80, samples y = 80, variable = \u, variable y = \v ] ( { \r*sin(u)*cos(v) }, { \r*cos(u) }, { \r*sin(u)*sin(v) } ); \end{axis} \end{tikzpicture} \end{document}
|
|
Eine einfache Umstellung von Grad auf Radiant ist vermutlich bisher nicht vorgesehen. Aber man kann sich zum Beispiel mittels \tikzset{ declare function={ sinr(\w)=sin(deg(\w)); cosr(\w)=cos(deg(\w)); } } Das kann man dann aber auch benutzen, um die gesamte Koordinatenangabe übersichtlicher zu machen und auch eine Parameteränderung zu erleichtern: \tikzset{ declare function={ a=.4;% Parameterangabe b=1-a^2; sinr(\w)=sin(deg(\w)); cosr(\w)=cos(deg(\w)); nenner(\u,\v)=(a*((sqrt(b)*cosh(a*\u))^2+ (a*sinr(sqrt(b)*\v))^2)); } } Damit ergibt sich der folgende Code: \documentclass[border=5pt]{standalone} \usepackage{pgfplots} \pgfplotsset{compat=1.8} \begin{document} \begin{tikzpicture} \tikzset{ declare function={ a=.4;% Parameter b=1-a^2; sinr(\w)=sin(deg(\w)); cosr(\w)=cos(deg(\w)); nenner(\u,\v)=(a*((sqrt(b)*cosh(a*\u))^2+ (a*sinr(sqrt(b)*\v))^2)); } } \begin{axis}[ view = {60}{-60}, hide axis, colormap = {flower}{% color(0cm) = (yellow); color(4cm) = (orange); color(8cm) = (red!40!black); color(12cm) = (red!80!black); color(16cm) = (green); color(20cm) = (green!20!black)}, ] \addplot3[ surf, z buffer = sort, point meta = u, domain = -13.2:13.2, domain y = -37.4:37.4, samples = 80, samples y = 120, variable = \u, variable y = \v ] ( { -u + (2*b*cosh(a*u)*sinh(a*u))/nenner(u,v) }, { (2*sqrt(b)*cosh(a*u) *(-(sqrt(b)*sinr(v)* cosr(sqrt(b)*v)) + cosr(v)*sinr(sqrt(b)*v))) /nenner(u,v) }, { (2*sqrt(b)*cosh(a*u) *(-(sqrt(b)*cosr(v)* cosr(sqrt(b)*v)) - sinr(v)*sinr(sqrt(b)*v))) /nenner(u,v) }); \end{axis} \end{tikzpicture} \end{document} Das Ergebnis für
(01 Jul '14, 10:30)
stefan ♦♦
|

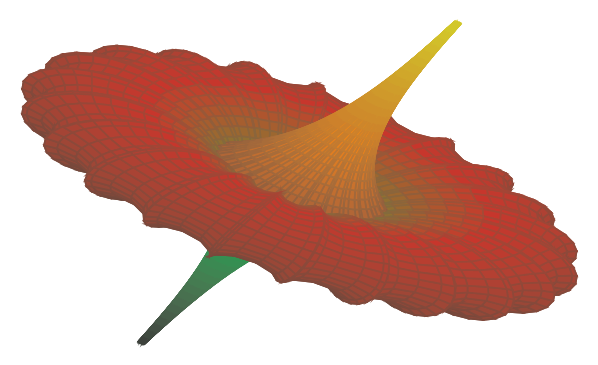


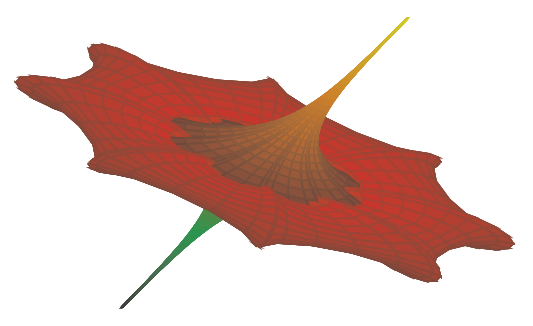
Mit LuaLaTeX aus MiKTeX 2.9 bekomme ich bei der Sample-Anzahl auch einen Fehler. Unter TL 2014 funktioniert das dagegen.