|
Ich versuche gerade, diesen Plot mit pgfplots zu generieren:
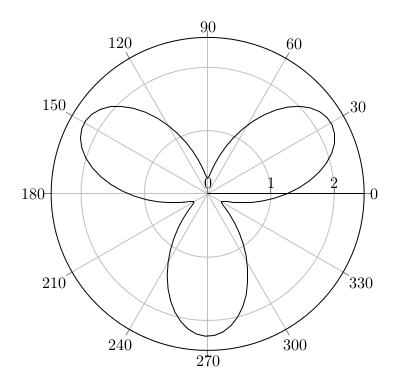
Ich sah eine aufschlussreiche Beschreibung auf Mathematica SE und gehe danach vor: zunächst den Querschnitt überlegen und dann drehen. Den Querschnitt gibt diese zweidimensionale Abbildung: \documentclass[border=10pt]{standalone} \usepackage{pgfplots} \usepgfplotslibrary{polar} \begin{document} \begin{tikzpicture} \begin{polaraxis} \addplot[mark=none, domain=0:360, samples=100] {sin(3*x) + 1.25}; \end{polaraxis} \end{tikzpicture} \end{document}
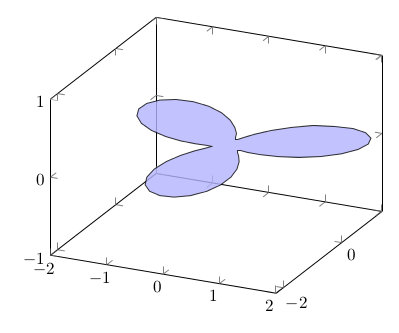
Diese stelle ich nun dreidimensional dar. Ich fülle die Fläche zur besseren Sicht einmal, und der Einfachheit halber bette ich sie auf die xy-Ebene. Am Ende kann man immer noch den Viewpoint ändern. \documentclass[border=10pt]{standalone} \usepackage{pgfplots} \begin{document} \begin{tikzpicture} \begin{axis} \addplot3 [domain=0:360, samples=60, fill=blue!30, opacity=0.8] ( {cos(x)*(sin(3*x) + 1.25)}, {sin(x)*(sin(3*x) + 1.25)}, 0 ); \end{axis} \end{tikzpicture} \end{document}
Die Transformation von polar auf kartesisch sieht man übrigens hier gut - das hatte ich zwischendurch als Stil für die Umrechnung (und alternativ \pgfplotsset{ polar/.style = { x filter/.code = \pgfmathparse{cos(deg(rawx))*rawy}, y filter/.code = \pgfmathparse{sin(deg(rawx))*rawy} } } Jetzt brauchen wir "nur" noch diesen Plot (ohne fill, opacity) im Kreis zu drehen und dabei um seinen Mittelpunkt rotieren. Das erstere Drehen hat Jake hier am Beispiel um die z-Achse im Prinzip beschrieben durch Plotten von Eine Mathematica-Version des Ganzen steht auf Mathematica.SE, siehe evtl. auch RotationTransform Referenz, falls obiges nicht genügt. Schafft jemand, das auf pgfplots zu adaptieren? |
|
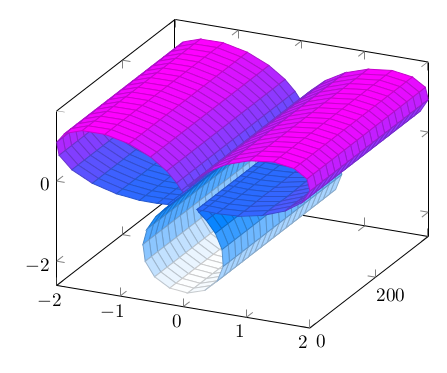
Auf TeX.SE gab cmhughes eine schöne Lösung. Ich hatte zunächst eine einfache 3D-Version entworfen mit \documentclass[border=10pt]{standalone} \usepackage{pgfplots} \begin{document} \begin{tikzpicture} \begin{axis} \addplot3 [ surf, domain = 0:360, y domain = 0:360, samples = 50, samples y = 20, ] ( {cos(x)*(sin(3*x) + 1.25)}, {y}, {sin(x)*(sin(3*x) + 1.25)} ); \end{axis} \end{tikzpicture} \end{document} welche das Objekt linear im Raum bewegt:
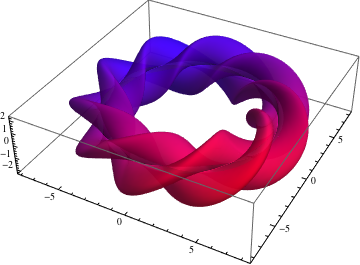
Da wir jedoch im Kreis drehen wollen, verarbeitete cmhughes die Tarametrisierung eines Torus, die für sich genommen beispielsweise so aussehen kann: x(t,s) = (2+cos(t))*cos(s+pi/2) y(t,s) = (2+cos(t))*sin(s+pi/2) z(t,s) = sin(t) Nutzen wir das für analog unsere Funktion: \documentclass[border=10pt]{standalone} \usepackage{pgfplots} \begin{document} \begin{tikzpicture} \begin{axis}[axis equal] \addplot3[ surf, domain = 0:360, y domain = 0:360, samples = 100, samples y = 70, z buffer = sort, colormap/cool, ] ( {(6+(sin(3*x)+1.25)*cos(x))*cos(y)}, {(6+(sin(3*x)+1.25)*cos(x))*sin(y)}, {((sin(3*x)+1.25)*sin(x))} ); \end{axis} \end{tikzpicture} \end{document}
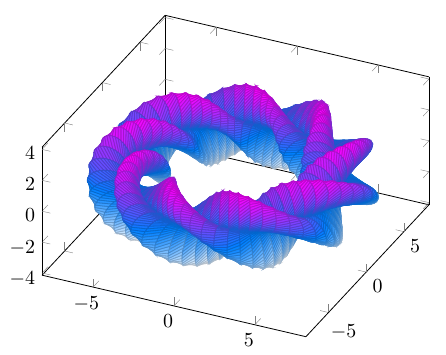
Jetzt brauchen wir nur noch eine Verdrehung um das Zentrum des Querschnitts, das erreichen wir durch Addieren eines Vielfachen von y, also unserem zweiten Drehwinkel, im Argument des ursprünglichen Funktionsteils: \documentclass[border=10pt]{standalone} \usepackage{pgfplots} \begin{document} \begin{tikzpicture} \begin{axis}[axis equal] \addplot3[ surf, domain = 0:360, y domain = 0:360, samples = 100, samples y = 70, z buffer = sort, colormap/cool, ] ( {(6+(sin(3*(x+3*y))+1.25)*cos(x))*cos(y)}, {(6+(sin(3*(x+3*y))+1.25)*cos(x))*sin(y)}, {((sin(3*(x+3*y))+1.25)*sin(x))} ); \end{axis} \end{tikzpicture} \end{document}
Um einmal zwei Stellschraube zu nennen: wählen wir in 3*y einen größeren Faktor, erhalten wir eine stärkere Verdrehung. Nehmen wir statt dem Summanden 6 zu Beginn einen größeren Wert, erhöht sich der horizontale Radius. Insgesamt ist das Ziel erreicht, eine zweidimensionale Funktion zu nehmen und sie in der dritten Dimension gleichzeitig in zwei Freiheitsgraden zu drehen. Wie lange dauert das Kompilieren?
(31 Jul '14, 15:58)
Johannes
@Johannes Fast eine Minute auf meinem Laptop. Ich habe LuaLaTeX verwendet, um keine Speicherprobleme zu kriegen.
(31 Jul '14, 16:23)
stefan ♦♦
Lualatex; Intel(R) Core(TM)2 Duo CPU T6670 @ 2.20GHz;
(31 Jul '14, 16:25)
Johannes
@Johannes LuaLaTeX, 2.3 GHz Intel Core i7 (mobiles Gerät), 16 GB RAM (viele Programme laufen nebenher), SSD-Laufwerk: real 0m53.013s user 0m52.795s sys 0m0.086s
(31 Jul '14, 16:34)
stefan ♦♦
Im Gegensatz zu TL2014 muss ich bei Verwendung von MiKTeX 2.9 (mal wieder) die sample Zahlen beim zweiten und dritten Beispiel verringern, damit es keine Speicherprobleme gibt.
(31 Jul '14, 16:49)
esdd
Ich denke, Du solltest
(03 Aug '14, 13:51)
cfeuersaenger
2
Was anderes: motiviert durch Dein Interesse an 3d surfaces und pgfplots (besonders auf dieser Seite) habe ich "Scalability and Performance" als Thema das aktuellen master branches von pgfplots gewaehlt. Ich habe einen prototyp, der Deinen Graph ohne aenderungen mehr als doppelt so schnell compiliert - und ich habe noch lange nicht alles potential ausgeschoepft (basiert auf einem echten LUA backend fuer pgfplots)
(03 Aug '14, 13:53)
cfeuersaenger
@cfeuersaenger Das ist ja großartig, vielen Dank! Man übersetzt denselben Graphen ja häufig für eine optimale Wahl an Domain, Samples, Shader und Blickperspektive. Da freue ich mich darauf, bald mit mehr Geschwindigkeit experimentieren zu können. Und spätere Leser können Ergebnisse dann auch einfacher reproduzieren.
(03 Aug '14, 16:01)
stefan ♦♦
Ergebnis 5 von 8
show 3 more comments
|


Zur Info, ich habe diese noch unbeantwortete Frage nun auch auf TeX.SE gepostet. Da kam auch eine Lösung, die ich bei Gelegenheit überarbeitet hier posten werde.