|
Verwandt mit wie-kann-ich-berechnete-koordinaten-punkte-aus-einer-schleife-verbinden Hallo!
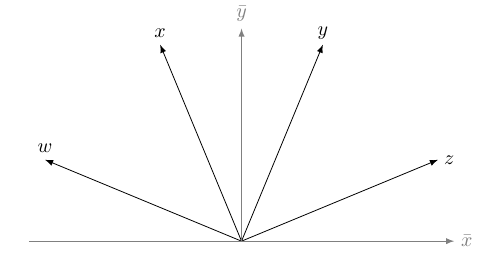
Wie kann ich vier eigene Koordinatenachsen definieren, so dass ich Punkte in der Form
\documentclass[a4paper]{amsart} \usepackage{selinput} \SelectInputMappings{adieresis={ä}, germandbls={ß}} \usepackage[ngerman]{babel} \usepackage{tikz} \usetikzlibrary{calc} \begin{document} % 4D-Graph ================== \def\beta{22.5} \begin{tikzpicture}[scale=2.5, >=latex, remember picture, ] %4D-Koordinatensystem: \draw[->] (0,0) -- ({1.5*cos(7*\beta)},{1.5*sin(7*\beta)}) node[above]{$w$}; \draw[->] (0,0) -- ({1.5*cos(5*\beta)},{1.5*sin(5*\beta)}) node[above]{$x$}; \draw[->] (0,0) --({1.5*cos(3*\beta)},{1.5*sin(3*\beta)}) node[yshift=2mm]{$y$}; \draw[->] (0,0) -- ({1.5*cos(\beta)},{1.5*sin(\beta)}) node[xshift=2mm]{$z$}; %2D-Zeichenebene \draw[->, gray] (-1.5,0) -- (1.5,0) node[right]{$\bar{x}$}; \draw[->, gray] (0,0) -- (0,1.5) node[above]{$\bar{y}$}; \end{document} |
|
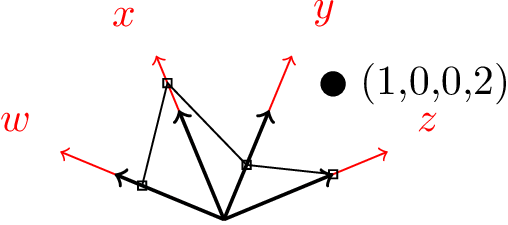
Ich habe ein Beispiel mit neuem Koordinatensystem vorbereitet. Da es sich bei (quat cs:w=<w>,x=<x>,y=<y>,z=<z>) wobei alle Einträge optional sind (ein leerer \documentclass{article} \usepackage{tikz} \begin{document} \makeatletter \tikzset{ cs/beta/.store in=\tikz@cs@beta, cs/w/.store in=\tikz@cs@w } \tikzdeclarecoordinatesystem{quat}% {% \tikzset{cs/.cd,beta=22.5,w=0,x=0,y=0,z=0,#1}% \pgfpointadd{\pgfpointxy{0}{0}}{% \pgfpointadd{\pgfpointpolarxy{7*\tikz@cs@beta}{\tikz@cs@w}}{% \pgfpointadd{\pgfpointpolarxy{5*\tikz@cs@beta}{\tikz@cs@x}}{% \pgfpointadd{\pgfpointpolarxy{3*\tikz@cs@beta}{\tikz@cs@y}}{% \pgfpointpolarxy{1*\tikz@cs@beta}{\tikz@cs@z}% }% }% }% }% } \def\beta{22.5} \begin{tikzpicture} \begin{scope}[red,->] \draw (0,0) -- ({1.5*cos(7*\beta)},{1.5*sin(7*\beta)}) node[label={7*\beta:$w$}] {}; \draw (0,0) -- ({1.5*cos(5*\beta)},{1.5*sin(5*\beta)}) node[label={5*\beta:$x$}] {}; \draw (0,0) -- ({1.5*cos(3*\beta)},{1.5*sin(3*\beta)}) node[label={3*\beta:$y$}] {}; \draw (0,0) -- ({1.5*cos(1*\beta)},{1.5*sin(1*\beta)}) node[label={1*\beta:$z$}] {}; \end{scope} \begin{scope}[thick,->] \draw (0,0) -- (quat cs:w=1); \draw (0,0) -- (quat cs:x=1); \draw (0,0) -- (quat cs:y=1); \draw (0,0) -- (quat cs:z=1); \end{scope} \draw[every node/.style={draw,inner sep=1pt}] (quat cs:w=0.75) node {} -- (quat cs:x=1.25) node {} -- (quat cs:y=0.5) node {} -- (quat cs:z=1) node {}; \node[draw,fill,circle,inner sep=2pt,label={right:(1,0,0,2)}] at (quat cs:w=1,z=2) {}; \end{tikzpicture} \end{document} |

Die Frage ist zwar schon fünf Jahre alt, aber will hier gleich mal anmerken, dass es soetwas wie ein "vierdimensionales" Koordinatensystem nicht gibt. In der oben beschriebenen Darstellung ist keine weitere vierte zu unserem Punkt senkrechte Gerade (Dimensionallinie) vorzufinden. Wir sehen hier lediglich weiterhin die Parallelprojektion eines dreidimensionalen Koordinatensystems. Alle Versuche ein vierdimensionales Koordinatensystem zu konstruieren müssen notwendigerweise fehlschlagen, eben da unser Anschauungsraum keine vier Senkrechte auf einem Punkt zulässt.
Ein vierdimensionales Koordinatensystem kann man verwenden, man sieht es natürlich nicht direkt in unserem Anschauungsraum, zeichnerisch könnte man es projizieren.