|
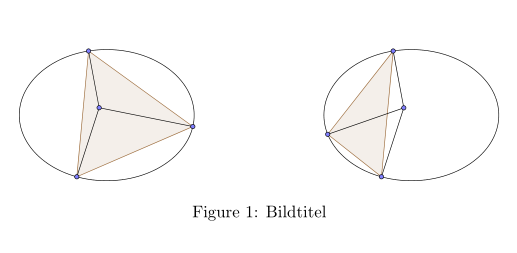
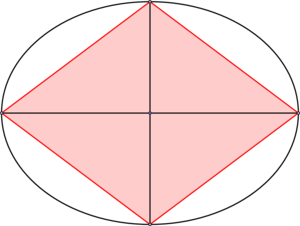
Ich habe zweimal die gleiche Ellipse gegeben und würde gerne Punkte darauf ansprechen, das Endresultat soll in etwa so aussehen:
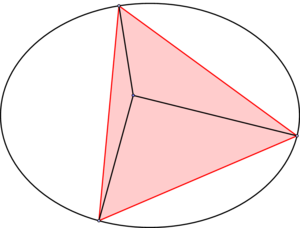
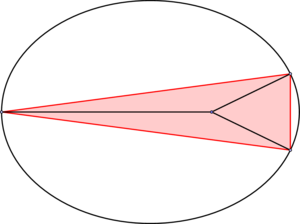
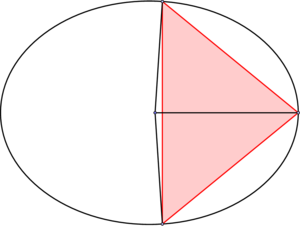
Dabei ist es wichtig, dass die Normalen sich einmal im Inneren der drei Punkte auf der Ellipse und einmal außerhalb schneiden. Das Problem ist, dass ich nicht weiß wie man Punkte auf einer Kurve (hier Ellipse) ansprechen kann, es soll sich aber in beiden Fällen um die gleiche Kurve handeln. \documentclass[a4paper,11pt]{article} \usepackage{tikz} \usepackage{subcaption} \usepackage{caption} \begin{document} \begin{figure}[htb] \centering \begin{minipage}[t]{.45\linewidth} \centering \begin{tikzpicture} %Normalen schneiden sich im Inneren des Dreiecks \draw (0, 0) ellipse (2 and 1.5); \end{tikzpicture} \end{minipage} \hfill \begin{minipage}[t]{.45\linewidth} \centering \begin{tikzpicture} %Normalen schneiden sich nicht im Dreieck \draw (0, 0) ellipse (2 and 1.5); \end{tikzpicture} \end{minipage} \caption{Bildtitel} \end{figure} \end{document} |
|
Das war jetzt aber fast mehr eine Matheaufgabe. Wenn man die Länge der Halbachse in x-Richtung mit
Code: \documentclass[a4paper,11pt]{article} \usepackage{tikz} \usetikzlibrary{ calc, math, intersections } \tikzset{ dot/.style={circle,draw,fill=blue!50,inner sep=1pt}, area/.style={draw=#1!80!black,fill=#1!80!black!10} } \newcommand\Ellipse[3]{% \begin{tikzpicture}[evaluate={\a=2;\b=1.5;}] \draw (0, 0) ellipse [x radius=\a,y radius=\b]; \foreach[count=\i] \t in {#1,#2,#3}{ \tikzmath{ \ex=\a*cos(\t); \ey=\b*sin(\t); \ny0=(\b^2-\a^2)/\b^2*sin(\t); } \path(\ex,\ey)coordinate(n\i); \path[name path global=l\i,overlay]($(0,\ny0)!-1!(n\i)$)--(n\i); } \path[area=brown](n1)--(n2)--(n3)--cycle; \path[name intersections={of=l1 and l2,by=ns}]; \foreach \i in {1,...,3}\draw (ns)--(n\i)node[dot]{}; \node[dot]at(ns){}; \end{tikzpicture}% } \begin{document} \begin{figure}[htb] \centering \begin{minipage}[t]{.45\linewidth} \centering \Ellipse{-10}{102}{250} \end{minipage}% \hfill \begin{minipage}[t]{.45\linewidth} \centering \Ellipse{102}{197}{250} \end{minipage} \caption{Bildtitel} \end{figure} \end{document} 1
Es gibt polare Koordinaten auch als
(02 Jun '15, 16:31)
Qrrbrbirlbel
|
|
Wie du sicherlich weißt, können Punkte auf einem Kreis („polare Koordinaten“) in TikZ angesprochen werden mit (<Winkel>:<Radius>) Dies ist die implizite Version des (xy polar cs: angle=<Winkel>, radius=<Radius>) bzw. (canvas polar cs: angle=<Winkel>, radius=<Radius mit Dimensionseinheit>) schreiben. Ich hatte in einer anderen Antwort schonmal was zu dem Unterschied zwischen Dort steht auch, dass es polare Koordinaten mit einem x- sowie einem y-Radius gibt, also: (<Winkel>:<x-Radius> and <y-Radius>) Es sei noch angemerkt, dass die circle (<Radius>) circle (<x-Radius> and <y-Radius>) ellipse (<Radius>) ellipse (<x-Radius> and <y-Radius>) als veraltet gilt. Ich spreche mich immer wieder gerne für die circle [radius=<Radius>] circle [x radius=<x-Radius>, y radius=<y-Radius>] ellipse [radius=<Radius>] ellipse [x radius=<x-Radius>, y radius=<y-Radius>] Diese haben nämlich den Vorteil, dass man Werte in einem Scope darüber (der Pfad selbst, eine \draw[radius=.5] (0,0) circle[] ++(right:1) circle[] (.5,1) circle[x radius=1]; Das TikZ-Handbuch spricht auch noch davon, dass die runden Klammern für Koordinaten vorgesehen sind. Nun zu deiner Frage: Ich schließe mich esdd an. Drei (nicht-triviale) Winkel finden, für die es einen gemeinsamen Normalenschnittpunkt gibt, ist eine Mathematik- und keine TikZ-Aufgabe. (Mal abgesehen davon, wenn die Grafik nur so aussehen soll wie deine Vorgabe, suche drei Winkel bei denen das halt ungefähr hinhaut, und gut ist. So präzise ist TikZ/PGF dann auch nicht.) Ich nutze in meiner Lösung tatsächlich aber kein einziges mal eine polare Koordinate, da ich zum Spezifizieren eines Punktes auf der Ellipse die Ich setze x- und y-Radius in den Optionen vom TikZpicture: \begin{tikzpicture}[x radius=2, y radius=1.5] Diese Angaben gelten sowohl für Das erlaubt mir jetzt also einfach \draw circle[];
und sowas wie \draw (0:x_radius) arc[start angle=0, end angle=<Winkel>] zu sagen, um einen Bogen zu beschreiben, der mich zu dem \path[start angle=0] \foreach \winkel[count=\zaehler] in {<Liste von Winkeln>}{ (0:x_radius) arc [end angle=\winkel] coordinate (e\zaehler-c) -- ([turn]90:1) coordinate (e\zaehler-norm-c) } coordinate (eC) at (intersection of e1-c--e1-norm-c and e2-c--e2-norm-c); Die Koordinate Danach wird in ähnlicher Schleifen-Weise das Drei- oder n-Eck gezeichnet, die \fill[nodes={dot=blue!25}, fill=red!20, draw=red] (e1-c) \foreach \winkel[count=\zaehler] in {<Liste von Winkeln>}{ -- (e\zaehler-c) node(e\zaehler-n)[]} -- cycle node (eC-n) at(eC) [dot=blue!50] \foreach \winkel[count=\zaehler] in {<Liste von Winkeln>} {edge[black] (e\zaehler-n)}; Code\documentclass[tikz]{standalone} \newcommand*\tvo[1]{\pgfkeysvalueof{/tikz/#1}} \tikzset{ declare function={x_radius=\tvo{x radius};y_radius=\tvo{y radius};}, dot/.style={circle, draw=black, fill={#1}, inner sep=+0pt, minimum size=+1pt, very thin, node contents=}, } \newcommand*\Ellipse[2][]{% \begin{tikzpicture}[ x radius=2, y radius=1.5,#1] \draw circle[]; \path[start angle=0] \foreach \winkel[count=\zaehler] in {#2}{ (0:x_radius) arc [end angle=\winkel] coordinate (e\zaehler-c) -- ([turn]90:1) coordinate (e\zaehler-norm-c) } coordinate (eC) at (intersection of e1-c--e1-norm-c and e2-c--e2-norm-c); \fill[nodes={dot=blue!25}, fill=red!20, draw=red] (e1-c) \foreach \winkel[count=\zaehler] in {#2}{ -- (e\zaehler-c) node(e\zaehler-n)[]} -- cycle node (eC-n) at(eC) [dot=blue!50] \foreach \winkel[count=\zaehler] in {#2} {edge[black] (e\zaehler-n)}; \end{tikzpicture}} \begin{document} \Ellipse{349.5, 102, 250} \Ellipse{20, 180, 360-20} \Ellipse[line join=bevel]{85, 360, 360-85} \Ellipse{90, 180, 270, 360} \end{document} Output
|