Wie kann ich in TikZ eine Strecke bis zu einer anderen Strecke verlängern?

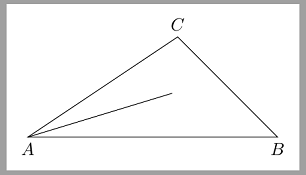
Ich hab hier ein komplexes Beispiel. Ich möchte die Winkelhalbierende bis zur gegenüberliegenden Dreiecksseite verlängern.

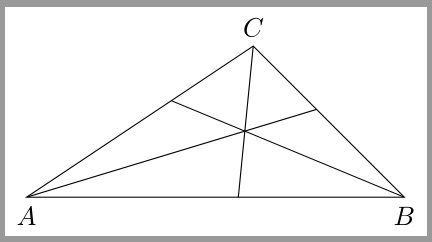
alt text

Wenn das Beispiel zu aufwendig ist, kann ich auch ein minimaleres Beispiel erstellen.

Open in Online-Editor

Code, hier editierbar zum Übersetzen:


 
 
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

linien tikz schnittpunkte

gefragt 21 Jun '16, 16:05

cis
9.6k●103●460●491
Akzeptiert-Rate: 29%

bearbeitet 21 Jun '16, 17:50

saputello
11.1k●17●43●65

Eine Antwort:

active answers älteste Antworten neueste Antworten Beliebteste Antworten

Eine Möglichkeit wäre path picture für den Dreieckspfad zu verwenden. Dann kann man die Linie beliebig weit über W hinaus verlängern. Sie wird trotzdem nur innerhalb des Dreiecks gezeichnet und beeinflusst damit auch nicht die Bounding Box.

Open in Online-Editor

Code, hier editierbar zum Übersetzen:


 
 
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

Wenn man das Dreieck noch nicht gezeichnet hat, kann man das hier mit erledigen lassen.

Open in Online-Editor

Code, hier editierbar zum Übersetzen:


 
 
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

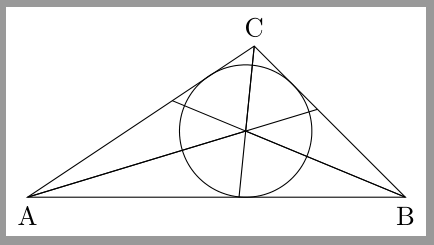
alt text

Und mal noch eine mögliche Alternative für das ganze Beispiel:

Open in Online-Editor

Code, hier editierbar zum Übersetzen:


 
 
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

alt text

Permanenter link

beantwortet 21 Jun '16, 19:52

esdd
17.8k●30●42●57
Akzeptiert-Rate: 62%

bearbeitet 21 Jun '16, 19:57

Klasse! Doch nicht so ein triviales Problem, wie ich anfangs dachte.

(21 Jun '16, 22:47) cis

Deine Antwort

[Vorschau ausblenden]

Community Wiki:

Folgen dieser Frage

Per E-Mail:

Wenn sie sich anmelden, kommen Sie für alle Updates hier in Frage

Per RSS:

Antworten

Antworten und Kommentare

Frage-Themen:

tikz ×731
linien ×30
schnittpunkte ×6

gestellte Frage: 21 Jun '16, 16:05

Frage wurde gesehen: 7,205 Mal

zuletzt geändert: 21 Jun '16, 22:47

Wie kann ich in TikZ eine Strecke bis zu einer anderen Strecke verlängern?

Folgen dieser Frage

verwandte Fragen