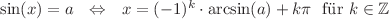|
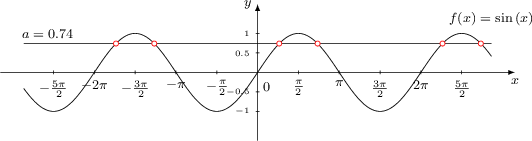
Hallo! Ich habe jetzt kürzlich einen TikZ-Graphen für die Gleichung sin(x) = a erstellt.
Die Berechnungsformel lautet:
Link zum Artikel mit Herleitung: Lösung der Gleichung sin(x) = a für a ∈ [-1,1]. Mir geht es um den Teil der Schnittpunkte: %Schnittpunkte \foreach \k in {-2,...,3}{%% % x-Wert berechnen und abspeichern \pgfmathparse{((-1)^\k) * 3.14159265359*asin(\a)/180 + \k*3.14159265359} \let\myresult\pgfmathresult \pgfmathparse{\myresult} \let\myresult\pgfmathresult \draw[color=red, fill=white] plot[mark=*,mark size=2.75pt] coordinates{ ( {\myresult}, {\a} ) }; %\node[] at (\myresult,\a) {\myresult}; }%% Hier konnte ich die Arkussinusfunktion Nun die Frage: Wäre der Graph bzw. die Rechnung ggf. auch einfacher gegangen? Am Rande: Auch hab ich es nicht geschafft die Zahl pi als Platzhalter reinzuschreiben - Hinweis: Ich nehme ganz gerne die plotmarks-Bibliothek, weil man da viele Optionen hat. Vollständiges Bsp.: \documentclass[varwidth, margin=2.5pt]{standalone} \usepackage[ngerman]{babel} \usepackage{tikz} \usetikzlibrary{plotmarks} \usepackage{amsmath, amssymb} %=========== \begin{document} %=========== \def\a{0.74} \begin{tikzpicture}[x = 1cm, y=1.5cm, scale=0.45, font=\footnotesize, >=latex %Voreinstellung für Pfeilspitzen ] % % Funktionen y = sin(x), y = a \draw[] plot[samples=300, domain=-9:9] (\x,{sin(\x r)}) node[above=15pt] {$f(x)=\sin\left(x\right)$}; \draw[] (9,\a) -- (-9,\a) node[above, xshift=5mm] {$a = \a$}; %Schnittpunkte \foreach \k in {-2,...,3}{%% % x-Wert berechnen und abspeichern \pgfmathparse{((-1)^\k) * 3.14159265359*asin(\a)/180 + \k*3.14159265359} \let\myresult\pgfmathresult \pgfmathparse{\myresult} \let\myresult\pgfmathresult \draw[color=red, fill=white] plot[mark=*,mark size=2.75pt] coordinates{ ( {\myresult}, {\a} ) }; %\node[] at (\myresult,\a) {\myresult}; }%% % Koordinatensystem % x-Achse \draw[->] (-9.9,0) -- (9.9,0) node[below] {$x$}; %Zahlen auf x-Achse \foreach \x/\xtext in { -.5*pi/-\frac{\pi}{2}, -pi/-\pi, -1.5*pi/-\frac{3\pi}{2}, -2*pi/-2\pi, -2.5*pi/-\frac{5\pi}{2}, .5*pi/\frac{\pi}{2}, pi/\pi, 1.5*pi/\frac{3\pi}{2}, 2*pi/2\pi, 2.5*pi/\frac{5\pi}{2} } \draw (\x,2pt) -- (\x,-2pt) node[below] {$\xtext$}; % y-Achse \draw[->] (0,-1.75) -- (0,1.75) node[left] {$y$}; %Zahlen auf y-Achse \foreach \y in {-1,-0.5,0.5,1} \draw[] (2pt,\y) -- (-2pt,\y) node[left] {\tiny $\y$}; %Ursprung \draw[] (0pt,-5pt) node[below right] {$0$}; \end{tikzpicture} %=========== \end{document} %=========== |
|
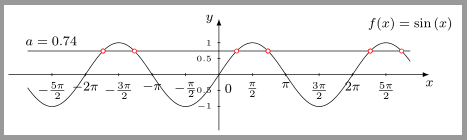
Da Du die Gleichung für die Berechnung der Schnittpunkte kennst, kannst Du diese direkt einsetzen. Das einzige, was man dabei beachten muss, ist, dass das Ergebnis von % Schnittpunkte \foreach \k in {-2,...,3} \draw[color=red, fill=white] plot[mark=*,mark size=2.75pt] coordinates{( {((-1)^\k) * rad(asin(\a)) + \k*pi}, {\a} )}; In dem Code siehst Du auch gleich, wie Du Wenn Du den Wert als %Schnittpunkte \foreach \k in {-2,...,3}{ \pgfmathsetmacro\myresult{((-1)^\k) * rad(asin(\a)) + \k*pi} \draw[color=blue, fill=white] plot[mark=*,mark size=2.75pt] coordinates{( {\myresult}, {\a} )}; } Zum Ermitteln der Schnittpunkte kann man auch die Bibliothek % y = sin(x), sin(x) = a \def\a{0.74} % Funktionen \draw[name path=plot] plot[samples=300, domain=-9:9] (\x,{sin(\x r)}) node[above=15pt] {$f(x)=\sin\left(x\right)$}; \draw[name path=a] (9,\a) -- (-9,\a) node[above, xshift=5mm] {$a = \a$}; % Schnittpunkte \draw[red,fill=white,name intersections={of=plot and a,name=i, total=\i}] \foreach\s in {1,...,\i}{plot[mark=*,mark size=2.75pt] coordinates{(i-\s)}};
Code: \documentclass[varwidth, margin=2.5pt]{standalone} \usepackage[ngerman]{babel} \usepackage{tikz} \usetikzlibrary{plotmarks} \usetikzlibrary{intersections} \usepackage{amsmath, amssymb} \begin{document} \begin{tikzpicture}[x = 1cm, y=1.5cm, scale=0.45,font=\footnotesize,>=latex] % y = sin(x), sin(x) = a \def\a{0.74} % Funktionen \draw[name path=plot] plot[samples=300, domain=-9:9] (\x,{sin(\x r)}) node[above=15pt] {$f(x)=\sin\left(x\right)$}; \draw[name path=a] (9,\a) -- (-9,\a) node[above, xshift=5mm] {$a = \a$}; % Schnittpunkte \draw[red,fill=white,name intersections={of=plot and a,name=i, total=\i}] \foreach\s in {1,...,\i}{plot[mark=*,mark size=2.75pt] coordinates{(i-\s)}}; % x-Achse \draw[->] (-9.9,0) -- (9.9,0) node[below] {$x$}; %Zahlen auf x-Achse \foreach \x/\xtext in {% -.5*pi/-\frac{\pi}{2}, -pi/-\pi, -1.5*pi/-\frac{3\pi}{2}, -2*pi/-2\pi, -2.5*pi/-\frac{5\pi}{2}, .5*pi/\frac{\pi}{2}, pi/\pi, 1.5*pi/\frac{3\pi}{2}, 2*pi/2\pi, 2.5*pi/\frac{5\pi}{2}% }\draw (\x,2pt) -- (\x,-2pt) node[below] {$\xtext$}; % y-Achse \draw[->] (0,-1.75) -- (0,1.75) node[left] {$y$}; %Zahlen auf y-Achse \foreach \y in {-1,-0.5,0.5,1}\draw (2pt,\y) -- (-2pt,\y) node[left] {\tiny $\y$}; %Ursprung \draw(0pt,-5pt) node[below right] {$0$}; \end{tikzpicture} \end{document} Ah ok, inzwischen kann
(05 Feb '15, 13:02)
cis
@cis Das mit der Rechnung habe ich jetzt noch ergänzt. Das geht wesentlich einfacher als in Deinem MWE ;-)
(05 Feb '15, 13:29)
esdd
Ahja, sehr gut! Solche Rechnungen kann man an anderer Stelle sicher auch oft brauchen! ;)
(05 Feb '15, 13:47)
cis
|