|
Ich suche ein Möglichkeit, Winkel mit einem gegebenen Maß einzuzeichnen:
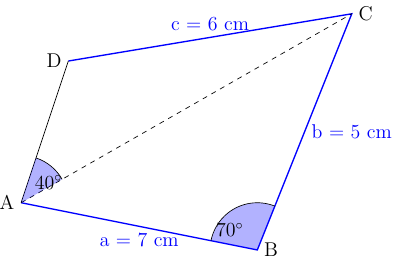
Ich habe zunächst das Dreieck ABC gezeichnet, aber um den 40 Grad Winkel bei A einzeichnen zu können, müsste ich erst den unteren Teilwinkel bei A berechnen, um dann mit einer Polarkoordinate weiterzuarbeiten. Gibt es eine Möglichkeit, dieses Viereck zu zeichnen, OHNE irgendwelche Werte berechnen zu müssen? Kann man also Polarkoordinaten auch bezüglich einer anderen Nulllinie angeben? Mein Code so weit: \documentclass[10pt,a4paper]{article} \usepackage[utf8]{inputenc} \usepackage[german]{babel} \usepackage{tikz} \begin{document} \begin{tikzpicture} \coordinate[label=left:A] (A) at (0,0); \coordinate[label=right:B] (B) at (7,0); \draw (A)--(B)--++(110:5cm) coordinate[label=right:C] (C); \end{tikzpicture} \end{document} |
|
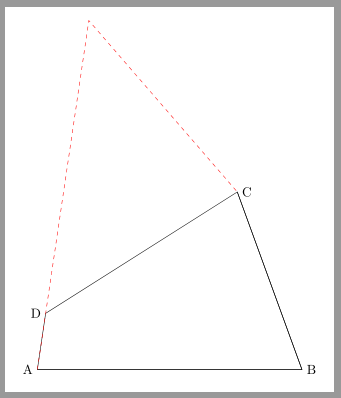
Eine Möglichkeit wäre die Damit das Vierecke gezeichnet werden kann, muss aber der Schnittpunkt zwischen einer Linie von A zu diesem Hilfspunkt und einem Kreis mit Durchmesser von 6cm um C ermittelt werden. Dafür lässt sich die Es gibt übrigens zwei Vierecke, die die Anforderungen erfüllen. \documentclass[margin=10pt]{standalone} \usepackage{tikz} \usetikzlibrary{ calc, intersections } \begin{document} \begin{tikzpicture} \path (0,0)coordinate[label=left:A](A) (7,0)coordinate[label=right:B](B) +(110:5) coordinate[label=right:C] (C); \path[name path=linie,overlay](A)--($(A)!2!40:(C)$); \path[name path=kreis,overlay](C)circle[radius=6]; \path[name intersections={of=linie and kreis,sort by=linie,name=schnittpunkt}]; \coordinate[label=left:D] (D) at (schnittpunkt-1); \draw(A)--(B)--(C)--(D)--cycle; \draw[red,dashed](A)--(schnittpunkt-2)--(C); \end{tikzpicture} \end{document}
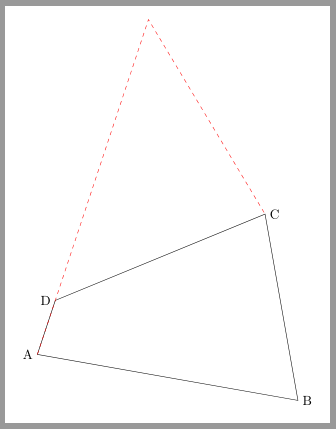
Alternativ kann man auch die \documentclass[margin=10pt]{standalone} \usepackage{tikz} \usetikzlibrary{intersections} \begin{document} \begin{tikzpicture} \path (0,0)coordinate[label=left:A](A) (-10:7)coordinate[label=right:B](B) ([turn]110:5) coordinate[label=right:C] (C);% 180-70=110 \path[overlay](C)--(A) ([turn]-140:25)coordinate(H);% -180+40=-140 \path[name path=linie,overlay](A)--(H); \path[name path=kreis,overlay](C)circle[radius=6]; \path[name intersections={of=linie and kreis,sort by=linie,name=schnittpunkt}]; \coordinate[label=left:D] (D) at (schnittpunkt-1); \draw(A)--(B)--(C)--(D)--cycle; \draw[red,dashed](A)--(schnittpunkt-2)--(C); \end{tikzpicture} \end{document}
Super, das ist genau das was ich gesucht habe. Dass es zwei mögliche Vierecke gibt, ist sozusagen Absicht... Vielen Dank
(10 Apr '15, 12:37)
Astrina
|