|
Bei folgendem Beispiel musste ich die Elemente so eingeben
die Eingabe
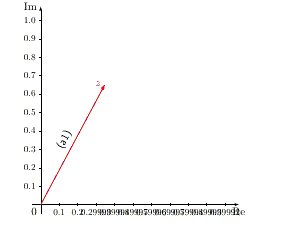
führte zu einem seltsamen Ergebnis (siehe Bild). Wie kann ich das beheben?
\documentclass[]{scrartcl} \usepackage{tikz} \begin{document} \begin{tikzpicture}[ %font=\footnotesize, >=latex, scale=0.65, x=10cm, y=10cm, ] %KoSy %Gitternetzlinien %\draw[very thin,color=gray] (-2,-4) grid (3,4); %Achsen \draw[->] (-0.05,0) -- (1.075,0) node[right, below] {Re}; \draw[->] (0,-0.05) -- (0,1.075) node[above, left] {Im}; %Achsenbeschriftung %Zahlen auf x-Achse \foreach \x in {0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0} { \if\x0\else \draw (\x,2pt) -- (\x, -2pt) node[below, font=\footnotesize] {$\x$}; \fi} %Zahlen auf y-Achse \foreach \y in {0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0} { \if\y0\else \draw (2pt,\y) -- (-2pt,\y) node[left, font=\footnotesize]{$\y$}; \fi} %Ursprung \node[below left] {$0$}; %Funktionen \def\a{0.3482759645} \def\b{0.6517240354} \coordinate(O) at (0,0); \coordinate(Z) at (\a,\b); \coordinate(W) at (\b,\a); \coordinate(ZplusW) at (\a+\b,\b+\a); \coordinate(absZi) at (0,\a^2+\b^2); %z=a+ib \draw[red, thick, ->] (O) -- (Z) node[sloped, above, midway, text=black, font=\sffamily]{(a1)} node[left]{$z$}; \end{tikzpicture} \end{document} |
|
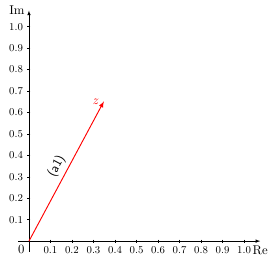
Das ist ein Rundungsproblem, das in der \documentclass{scrartcl} \usepackage{tikz} \begin{document} \begin{tikzpicture}[ %font=\footnotesize, >=latex, scale=0.65, x=10cm, y=10cm, ] %KoSy %Gitternetzlinien %\draw[very thin,color=gray] (-2,-4) grid (3,4); %Achsen \draw[->] (-0.05,0) -- (1.075,0) node[right, below] {Re}; \draw[->] (0,-0.05) -- (0,1.075) node[above, left] {Im}; %Achsenbeschriftung %Zahlen auf x-Achse \foreach \x in {0.1,0.2,...,1} { \pgfkeys{/pgf/number format/.cd,fixed,fixed zerofill,precision=1} \draw (\x,2pt) -- (\x, -2pt) node[below, font=\footnotesize] {$\pgfmathprintnumber{\x}$}; } %Zahlen auf y-Achse \foreach \y in {0.1,0.2,...,1.0} { \pgfkeys{/pgf/number format/.cd,fixed,fixed zerofill,precision=1} \draw (2pt,\y) -- (-2pt,\y) node[left, font=\footnotesize]{$\pgfmathprintnumber{\y}$}; } %Ursprung \node[below left] {$0$}; %Funktionen \def\a{0.3482759645} \def\b{0.6517240354} \coordinate(O) at (0,0); \coordinate(Z) at (\a,\b); \coordinate(W) at (\b,\a); \coordinate(ZplusW) at (\a+\b,\b+\a); \coordinate(absZi) at (0,\a^2+\b^2); %z=a+ib \draw[red, thick, ->] (O) -- (Z) node[sloped, above, midway, text=black, font=\sffamily]{(a1)} node[left]{$z$}; \end{tikzpicture} \end{document}
Ohne die Einstellung einer festen Anzahl an Nachkommastellen einschließlich Füllung mit Nullstellen via Ich habe in dem Beispiel außerdem die Fallunterscheidung, ob |