|
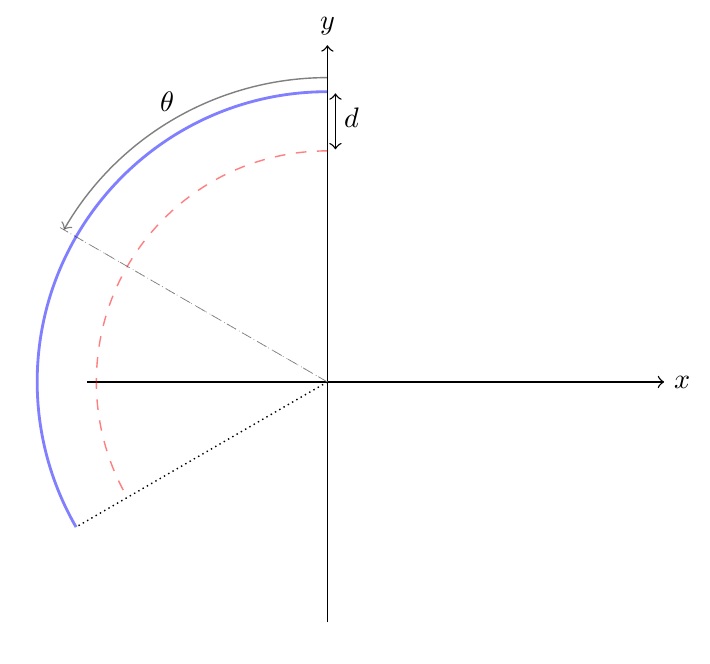
Bei dem nachkommenden Bild möchte ich dazu eine Kurve im Schwarz plotten, die mathemathisch durch diese Funktion beschreibbar ist: F = C - d * Cos(3/2*(theta - 60)) F: gezielte Funktion C: die blaue Kurve d: der Unterschied zw. blauen und roten Kurven \documentclass{article} \usepackage{tikz} \usetikzlibrary{matrix} \begin{document} \begin{tikzpicture}[scale=0.8, transform shape] \draw[->] (-3,0) -- (4.2,0) node[right] {$x$}; \draw[->] (0,-3) -- (0,4.2) node[above] {$y$}; \draw[<->] (0.1,2.9) -- (0.1,3.6); \draw[densely dotted] (0,0) -- (0,3.85); \draw[densely dashed] (0,0) -- (0,3.85); \draw[densely dotted, rotate=120] (0,0) -- (0,3.60); \draw[densely dotted, style=help lines, rotate=60] (0,0) -- (0,3.85); \draw[densely dashed, style=help lines, rotate=60] (0,0) -- (0,3.85); \draw[thick,blue,opacity=0.5] ([shift=(90:103pt)]0,0) arc (90:210:103pt); \draw[red,dashed,opacity=0.5] ([shift=(90:82pt)]0,0) arc (90:210:82pt); \draw[->,black,opacity=0.5] ([shift=(90:108pt)]0,0) arc (90:150:108pt); \node (a) at (0.3,3.3) {$d$} node (b) at (-2,3.5) {$\theta$}; \end{tikzpicture} \end{document}
|
|
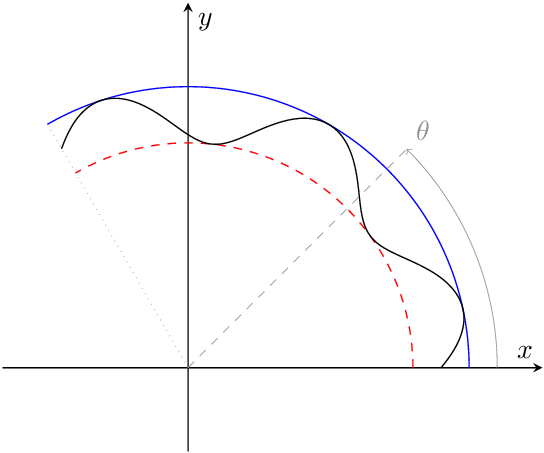
Mit \documentclass{article} \usepackage{pgfplots} \begin{document} \begin{tikzpicture} \begin{axis} [ % Plot settings domain=0:120, samples=101, no markers, smooth, % Axis settings axis equal, axis lines=middle, enlargelimits=true, xlabel=$x$, ylabel=$y$, xtick=\empty, ytick=\empty, ] \def\rb{5} \def\rr{4} % Circles \addplot[blue] ({\rb*cos(x)},{\rb*sin(x)}); \addplot[red,dashed] ({\rr*cos(x)},{\rr*sin(x)}); % Gray lines \addplot[help lines,->,domain=0:45] ({(\rb+.5)*cos(x)},{(\rb+.5)*sin(x)}) node [above right] {$\theta$}; \addplot[help lines,dashed,domain=0:1] ({x*(\rb+.5)*cos(45)},{x*(\rb+.5)*sin(45)}); \addplot[help lines,dotted,domain=0:1] ({x*\rb*cos(120)},{x*\rb*sin(120)}); % Plot in between \addplot[black] ( {( \rr + .5*(\rb-\rr)*( 1+cos(5*3/2*(x-60)) ) )*cos(x)}, {( \rr + .5*(\rb-\rr)*( 1+cos(5*3/2*(x-60)) ) )*sin(x)} ); \end{axis} \end{tikzpicture} \end{document}
Wäre hier Polarkoordinaten sinnvoll? (Ich habe die Frage glaub ich aber auch noch nicht ganz verstanden)
(12 Jan '17, 17:09)
stefan ♦♦
|
|
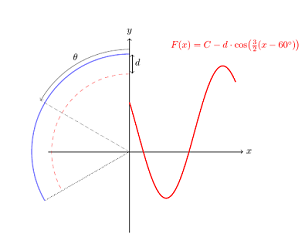
Mit TikZ so: %%%%%%%%%%%%%%%% %Funktion %%%%%%%%%%%%%%%% %F = C - d * Cos(3/2*(theta - 60)) %F: gezielte Funktion %C: die blaue Kurve %d: der Unterschied zw. blauen und roten Kurven \def\CWert{0.73} \def\dWert{2.45} \def\phiWert{60} \def\omegaWert{1.5} \draw[color=red, thick] plot[domain=0:1.25*pi, samples=200] ( {\x}, {\CWert - \dWert*cos(\omegaWert*(\x - \phiWert) r)} % r für "radiant" ) node[above=1cm]{$F(x) = C-d\cdot\cos\bigl(\frac32 (x - 60^\circ)\bigr)$} ;
\documentclass{article} \usepackage[ngerman]{babel} \usepackage{tikz} \usetikzlibrary{matrix} \begin{document} \begin{tikzpicture}[scale=0.8, transform shape] \draw[->] (-3,0) -- (4.2,0) node[right] {$x$}; \draw[->] (0,-3) -- (0,4.2) node[above] {$y$}; \draw[<->] (0.1,2.9) -- (0.1,3.6); \draw[densely dotted] (0,0) -- (0,3.85); \draw[densely dashed] (0,0) -- (0,3.85); \draw[densely dotted, rotate=120] (0,0) -- (0,3.60); \draw[densely dotted, style=help lines, rotate=60] (0,0) -- (0,3.85); \draw[densely dashed, style=help lines, rotate=60] (0,0) -- (0,3.85); \draw[thick,blue,opacity=0.5] ([shift=(90:103pt)]0,0) arc (90:210:103pt); \draw[red,dashed,opacity=0.5] ([shift=(90:82pt)]0,0) arc (90:210:82pt); \draw[->,black,opacity=0.5] ([shift=(90:108pt)]0,0) arc (90:150:108pt); \node (a) at (0.3,3.3) {$d$} node (b) at (-2,3.5) {$\theta$}; %%%%%%%%%%%%%%%% %Funktion %%%%%%%%%%%%%%%% %F = C - d * Cos(3/2*(theta - 60)) %F: gezielte Funktion %C: die blaue Kurve %d: der Unterschied zw. blauen und roten Kurven \def\CWert{0.73} \def\dWert{2.45} \def\phiWert{60} \def\omegaWert{1.5} \draw[color=red, thick] plot[domain=0:1.25*pi, samples=200] ( {\x}, {\CWert - \dWert*cos(\omegaWert*(\x - \phiWert) r)} % r für "radiant" ) node[above=1cm]{$F(x) = C-d\cdot\cos\bigl(\frac32 (x - 60^\circ)\bigr)$} ; \end{tikzpicture} \end{document} |

"Danke" etc. sind Dinge, die wir hier nicht benötigen und nach den Tipps zum Verfassen, die während der Eingabe der Frage in der Spalte rechts angezeigt werden, unterbleiben sollten. Auch die Frage, ob jemand helfen kann, ist eine überflüssige Selbstverständlichkeit. Wenn Du keine Hilfe wolltest, bräuchtest Du ja keine Frage zu stellen. Wir lieben es hier einfach kurz und knackig: Frage mit Beispiel und notwendigen Erläuterungn → Antwort, fertig.
Das ist nicht böse gemeint, aber verzichte bitte künftig einfach auf dergleichen.
BTW: Zum Plotten würde ich eher
pgfplotsverwenden (und dann ggf. umgekehrt in den Plot die beiden Radien und den Winkel einfügen. Wie genau? Müsste ich mir erst erarbeiten.Geht das überhaupt? Die blaue Kurve ist doch gar keine Funktion. Sie hat für ein und dasselben x links zwei verschiedene y-Werte. Ich habe vor rund 35 Jahren in der Schule noch gelernt, dass so etwas keine Funktion ist. Also könnte man C allenfalls als Koordinatenpaare interpretieren. Dann ist aber die Frage, was ein Koordinatenpaar abzüglich einer Zahl, die sich ja aus
d * Cos(3/2*(theta - 60))ergeben würde, sein soll. Desweiteren müsste man natürlichthetaunddkennen, um etwas berechnen zu können. Aber vielleicht reichen meine Mathekenntnisse auch einfach nicht.@saputello die Radien sind mir erstmal egal, hauptsächlich zwei Kreisteile mit auf einander liegendem Mittelpunkt und verschiedenen Radien in einem Theta-Bereich von 0 bis 120 Grad und dann die genannte Funktion zwischen den beiden.