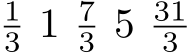Wie kann ich zwei tikzmath Rechnungen verschachteln?

Ich berechne im 1. Schritt die Glieder einer Folge.

Nun sollen die Folgenglieder durtch einen festgelegten Divisor geteilt werden, wobei eventuelle entstehende Ganzzahlen auch als Ganzzahl ausgegeben werden; Brüche werden voll gekürzt.

Wie kann ich Folgenglieder auf Bruchrechnung anwenden? Was muss ich da anders machen?

Öffne in Overleaf

Code, hier editierbar zum Übersetzen:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
\documentclass[11pt]{scrartcl}
%\documentclass[border=3mm]{standalone}
\usepackage[ngerman]{babel}
\usepackage{pgf, pgffor, tikz, amsmath, amssymb}
\usetikzlibrary{math, matrix}
\begin{document}
$M_n(k) = (2k-1)\cdot 2^n - 1 \text{ mit } k,n \in \mathbb{N}_{\geq 1}$ \\
%  \Mersenne{<k>}{<n>}  Folgenglieder berechnen
\newcommand{\Mersenne}[2]{% ===================
\tikzmath{% ===================
int \M, \n, \k;
for \k in {#1}{%
for \n in {#2}{%%
\M = (2*\k-1)*2^\n-1;
print {\M};  
};%%
};%
}     % ===================
}% ===================
 Test Mersenne: \Mersenne{1}{2}         %Test
\bigskip
%  Reduzierte Brüche / Ganzzahlen ausgeben
\newcommand{\rfrac}[2]{%%%%%%%%%%%%%%%%%%%%%%%
\begingroup
\tikzmath{%==================
int \Zaehler, \Nenner, \ggt, \Numerator, \Denominator;
\Zaehler = #1;          
\Nenner = #2;           
function GCD(\x,\y) {return gcd(\x,\y);};
\ggt = GCD(\Zaehler, \Nenner);
\Numerator = \Zaehler/\ggt;
\Denominator = \Nenner/\ggt;
if \Denominator == 1 then {
    print {$\Numerator$};
}
else { 
    print {$\dfrac{\Numerator}{\Denominator}$}; 
};
 
 
הההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההה
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

tikzmath tikz math

gefragt 03 Jan '18, 14:35

cis
9.6k●104●461●491
Akzeptiert-Rate: 29%

bearbeitet 03 Jan '18, 14:36

Eine Antwort:

active answers älteste Antworten neueste Antworten Beliebteste Antworten

Mit LuaLaTeX.

Öffne in Overleaf

Code, hier editierbar zum Übersetzen:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
\documentclass{article}
\usepackage{amsmath}
\usepackage{luacode}
\begin{luacode*}
-- https://de.wikipedia.org/wiki/Euklidischer_Algorithmus
local function gcd(a,b)
   return (b ~= 0) and gcd(b,a%b) or a
end
function reduce(a,b)
   local c = gcd(a,b)
   local a = a/c
   local b = b/c
   if (b == 1) then
      tex.sprint(a)
   else
      tex.sprint("\\frac{" .. a .. "}{" .. b .. "}")
   end
end
function mersenne(k,n)
   local M = (2*k-1)*2^n-1
   tex.sprint(M)
end
\end{luacode*}
\newcommand\rfrac[2]{\directlua{reduce(#1,#2)}}
\newcommand\mersenne[2]{\directlua{mersenne(#1,#2)}}
\begin{document}
$\rfrac{\mersenne{1}{1}}{3}$
$\rfrac{\mersenne{1}{2}}{3}$
$\rfrac{\mersenne{1}{3}}{3}$
$\rfrac{\mersenne{1}{4}}{3}$
$\rfrac{\mersenne{1}{5}}{3}$
\end{document}
 
 
הההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההה
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

Permanenter link

beantwortet 03 Jan '18, 22:02

Henri
15.7k●13●39●43
Akzeptiert-Rate: 46%

bearbeitet 03 Jan '18, 22:06

Ja, ähhh, danke... Aber Du immer mit Deinem Lua :) Das muss doch auch mit pdflatex gehen?

(03 Jan '18, 22:14) cis

@cis :-) ich finde es gut, auch oft Lua-Lösungen zu sehen, auch weil man die neue einfache direkte Programmierung anhand konkreter Beispiele gut sieht. Vielleicht will man gar nicht mehr zu Makro-Expansions-"Programmierung" zurück wenn man die Lua-Schnittstelle erstmal gewohnt ist. ;-)

(03 Jan '18, 22:34) stefan ♦♦

Deine Antwort

[Vorschau ausblenden]

Community Wiki:

Folgen dieser Frage

Per E-Mail:

Wenn sie sich anmelden, kommen Sie für alle Updates hier in Frage

Per RSS:

Antworten

Antworten und Kommentare

Frage-Themen:

tikz ×731
tikzmath ×5
math ×4

gestellte Frage: 03 Jan '18, 14:35

Frage wurde gesehen: 5,435 Mal

zuletzt geändert: 03 Jan '18, 22:34

Wie kann ich zwei tikzmath Rechnungen verschachteln?

Folgen dieser Frage

verwandte Fragen