|
Mit Hilfe von Kann man da irgendetwas machen? Öffne in Overleaf
\documentclass[border=15mm, varwidth]{standalone} \usepackage{tikz} \usetikzlibrary{fpu} %\usepackage{fp} % nutzte auch nichts \begin{document} \foreach \Bruch in {233/19, 3/4, 10/2, 2/3,0.6666666}{ %\pgfkeys{/pgf/number format/.cd,fixed} \pgfkeys{/pgf/number format/.cd,frac,frac shift={1}} \Bruch \pgfmathparse{\Bruch} = \pgfmathresult = \pgfmathprintnumber[frac]{\pgfmathresult} = \pgfmathprintnumber[frac,frac whole=false]{\pgfmathresult}\\[1em] } \end{document} |
|
Zu groß für das Kommentarfeld. Ich habe eine Berechnung über den Öffne in Overleaf
\documentclass[margin=5mm, varwidth]{standalone} \usepackage{tikz, amsmath} \usetikzlibrary{fpu} \begin{document} \foreach \zahl in {-2.235}{% \pgfmathparse{\zahl} Zahl: \pgfmathsetmacro\Zahl{\pgfmathresult} \Zahl \\ Ganzteil: \pgfmathsetmacro\Int{int(\Zahl)} \Int \\ Bruchteil: \pgfmathsetmacro\Frac{frac(\Zahl)} \Frac \\ dim(Bruchteil): \pgfmathsetmacro\Dim{dim(frac(\Zahl))} \Dim \\ Zehnerpotenz: \pgfmathsetmacro\Zehnerpotenz{10^(\Dim-2)} \Zehnerpotenz \\ Ganzzahl: \pgfmathsetmacro\Ganzzahl{round(\Zahl*\Zehnerpotenz)} \Ganzzahl \\ ggT(Ganzzahl,Zehnerpotenz): \pgfmathsetmacro\GGT{gcd(\Ganzzahl,\Zehnerpotenz)} \GGT \\ Z{\"a}hler: \pgfmathsetmacro\Zaehler{int(abs(\Ganzzahl/\GGT))} \Zaehler \\ Nenner: \pgfmathsetmacro\Nenner{int(\Zehnerpotenz/\GGT)} \Nenner \\ Vorzeichentest: \pgfmathsetmacro\Sign{\Zahl<0 ? "-" : ""} \Sign \\ Ganzzahltest:\def\Bruch{\frac{\Zaehler}{\Nenner}}% \pgfmathsetmacro\Ergebnis{\Zahl==int(\Zahl) ? "\Zahl" : "\Bruch"} $\Ergebnis$ \\[1em] Bruch: $\displaystyle \Zahl =\Sign\Ergebnis$ } \end{document} 1
Tja. Wie ich schon mal erwähnte - die pgf math Bibliothek ist objektiv schlechter als die von expl3. "dimension too large" bekommt man da öfter.
(24 Okt '18, 19:17)
Ulrike Fischer
Mich würde besonders interessieren, wie
(24 Okt '18, 20:52)
cis
Wenn es mir im sinnvollen Mathe-Einsatz in LaTeX geht, nehme ich bestimmt nicht expl3, sondern gleich ein richtiges CAS wie Sage(TeX). Nö, ich hatte eben gedacht, vielleicht gibt es Einstellungen in pgfmath, die ich nicht kenne.
(26 Okt '18, 04:59)
cis
|

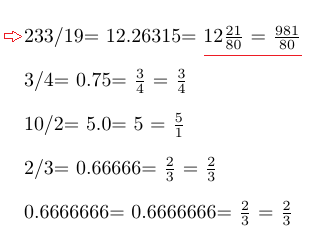

Was mich nur wundert:
polynom.styscheint mit heftigen Brüchen umgehen zu können,pgfmathdagegen nicht.https://tex.stackexchange.com/questions/180853/compute-denominator-and-numerator-of-irreducible-fraction-from-arbitrary-fractio
Ich kenne diesen Beitrag, ich weiß aber nicht, wie ich das hier anwenden kann.
Die Ergebnisse stimmen vorne und hinten nicht, denn 0.6666666 ist mit Sicherheit nicht gleich 2/3.
Klar, ich glaube ab
Null Komma <5 Sechsen>macht er daraus2/3.