|
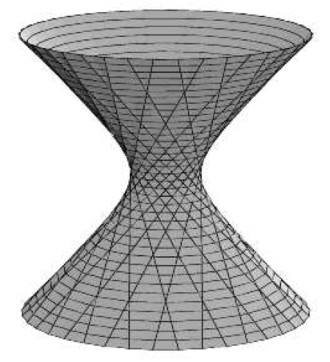
Ich würde gerne folgendes Bild tikzen:
allerdings weiß ich nicht genau wie. \documentclass{standalone} \usepackage{pgfplots} \pgfplotsset{compat=1.14} \begin{document} \begin{tikzpicture} \begin{axis}[ view={-25}{-25}, axis lines = middle, height = 12cm, width = 12cm, xmin=-4,xmax=5, ymin=-4,ymax=5, zmin=-2,zmax=3, xtick=\empty, ytick=\empty, ztick=\empty, xlabel={$x^{2}$}, ylabel={$x^{1}$}, zlabel={$t$}, ] % x^2+y^2-z^2=1 \addplot3[mesh,blue,domain=1:2,y domain=0:2*pi,samples=30]({x*cos(deg(y))},{x*sin(deg(y))},{sqrt(x^2-1)}); \addplot3[mesh,blue,domain=1:2,y domain=0:2*pi,samples=30]({x*cos(deg(y))},{x*sin(deg(y))},{-sqrt(x^2-1)}); % γ(θ)±(t):=a(0,cosθ,sinθ)+at(1,∓sinθ,±cosθ), % θ=0 \addplot3[red,thick,domain=-2:2,samples=30]({1-x*0},{0+x*1},{x}); \addplot3[red,thick,domain=-2:2,samples=30]({1+x*0},{0-x*1},{x}); % θ=pi \addplot3[red,thick,domain=-2:2,samples=30]({(-1)-x*0},{0+x*(-1),{x}}); \addplot3[red,thick,domain=-2:2,samples=30]({(-1)+x*0},{0-x*(-1),{x}}); % θ=pi/2 \addplot3[red,thick,domain=-2:2,samples=30]({0-x*1},{1+x*0},{x}); \addplot3[red,thick,domain=-2:2,samples=30]({0+x*1},{1-x*0},{x}); % θ=3pi/2 \addplot3[red,thick,domain=-2:2,samples=30]({0-x*(-1)},{(-1)+x*0},{x}); \addplot3[red,thick,domain=-2:2,samples=30]({0+x*(-1)},{(-1)-x*0},{x}); \end{axis} \end{tikzpicture} \end{document} Das ist mein Versuch. Es wäre auch schön ein 'grid' in der x-y Ebene zu haben. |
|
Ist zwar schon etwas her, aber ich habe einen Vorschlag. Dieser kann durchaus noch verbessert werden. Was stört, sind die Geraden. Da diese nach dem Hyperboloid gezeichnet werden, sieht man teilweise Geradenstücke, die eigentlich verdeckt sind. \documentclass{standalone} \usepackage{pgfplots} \pgfplotsset{compat=1.14} \begin{document} \begin{tikzpicture} \begin{axis}[ view={25}{20}, axis lines = none, height = 12cm, width = 12cm, xmin=-4,xmax=5, ymin=-4,ymax=5, zmin=-2,zmax=3, colormap = {hypo}{color(0cm) = (gray!30);color(1cm) = (gray!30)} ] % Koordinatenform x^2+y^2-z^2=1 %\addplot3[mesh,gray!30,domain=1:2,y domain=0:2*pi,samples=10]({x*cos(deg(y))},{x*sin(deg(y))},{sqrt(x^2-1)}); %surf,draw=black, %\addplot3[mesh,gray!30,domain=1:2,y domain=0:2*pi,samples=10]({x*cos(deg(y))},{x*sin(deg(y))},{-sqrt(x^2-1)}); % Parameterdarstellung mit hyperbolischen Funktionen % Parameter für elliptischen Hyperboloid (Bei a=b sind Schnittkurven Kreise) \def\a{1} \def\b{1} \def\c{1} \addplot3[surf,domain=0:1,y domain=0:2*pi,samples=30]({\a*cosh(x)*cos(deg(y))},{\b*cosh(x)*sin(deg(y))},{-\c*sinh(x)}); \addplot3[surf,domain=0:1,y domain=0:2*pi,samples=30]({\a*cosh(x)*cos(deg(y))},{\b*cosh(x)*sin(deg(y))},{\c*sinh(x)}); %%% Geradenschar: g_a(t):= (cos(a),sin(a),0)+t(-sin(a),cos(a),+-1) \foreach \i in {-150,-140,...,50} { \addplot3 [domain=-1.2:1.2,samples=10,black,thin] ( {cos(\i)-x*sin(\i)}, {sin(\i)+x*cos(\i)}, {x} ); \addplot3 [domain=-1.2:1.2,samples=10,black,thin] ( {cos(\i)-x*sin(\i)}, {sin(\i)+x*cos(\i)}, {-x} ); } \end{axis} \end{tikzpicture} \end{document} |

Willkommen auf TeXwelt!
Ich habe mir erlaubt, Deine Frage etwas zu ergänzen. Bitte beachte künftig die Tipps zum Verfassen rechts neben dem Eingabefeld für Fragen.
Crossposting: https://tex.stackexchange.com/questions/334448/functions-on-a-hyperboloid