|
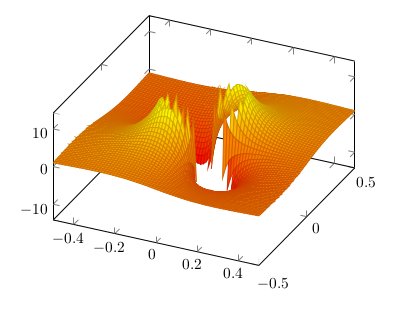
Ich möchte die Funktion x*y/(x^2+y^2)^2 plotten, die am Nullpunkt gegen unendlich geht. Daher möchte ich die Werte dort begrenzen, und mache das hier mit \documentclass{standalone} \usepackage{pgfplots} \usepgfplotslibrary{colormaps} \begin{document} \begin{tikzpicture} \begin{axis}[ restrict z to domain = -12:12, colormap/autumn, view/el = 45 ] \addplot3[ surf, samples = 70, domain = -0.5:0.5, domain y = -0.5:0.5, ] {x*y/(x^2+y^2)^2}; \end{axis} \end{tikzpicture} \end{document} Jedoch habe ich dann einen gezackten Rand:
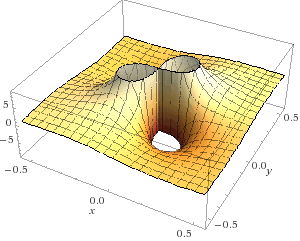
Ich möchte ihn gern gerade abgeschnitten haben, damit es vernünftig aussieht, etwas so (mit Wolfram Alpha):
Ideen, ggf. in Kombination:
Kam bei den Experimenten noch nix schönes raus. Wie kriege ich die Ränder gerade und den Plot ansehnlich, ähnlich wie im zweiten Plot? |
|
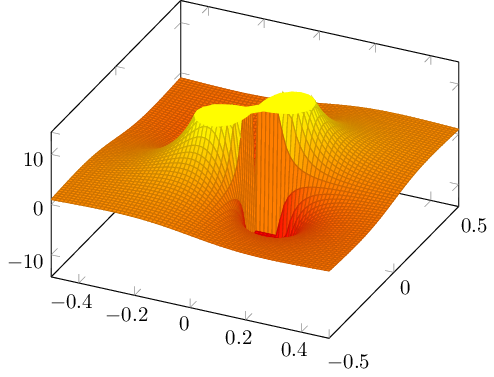
Das clippen scheint int diesem Beispiel mit Zum Zeichnen einer praeziseren Aussenkante kannst Du einen
\documentclass{standalone} \usepackage{pgfplots} \usepgfplotslibrary{colormaps} \begin{document} \begin{tikzpicture} \begin{axis}[ colormap/autumn, view/el = 45 ] \addplot3[ restrict z to domain* = -12:12, surf, samples = 70, domain = -0.5:0.5, domain y = -0.5:0.5, ] {x*y/(x^2+y^2)^2}; % the contour plot handler can *draw* a contour line, but it cannot fill: \addplot3[ contour gnuplot={ levels={12}, labels=false, }, samples = 70, domain = -0.5:0.5, domain y = -0.5:0.5, ] {x*y/(x^2+y^2)^2}; % now we fill the contour: \addplot3[ % 1000 is always the last entry in the colormap, i.e. point % meta max: /utils/exec={\pgfplotscolormapdefinemappedcolor{1000}}, draw=none, fill=mapped color] file {P_contourtmp0.table}; \end{axis} \end{tikzpicture} \end{document} Du kannst auch das fuellen weglassen und @cfeuersaenger Hervorragend, vielen Dank! Hab das gleich als Anlass zu einem Blogpost genommen: 3D-Plots beschneiden.
(19 Jul '14, 13:55)
stefan ♦♦
|