|
Folgender Code erlaubt nur Werte für
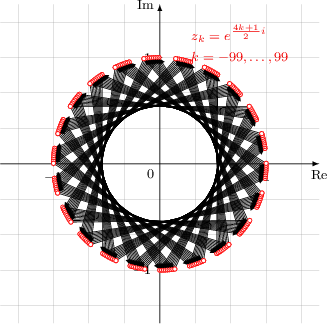
\documentclass[tikz, border=3mm]{standalone} %\documentclass{article} \usepackage[ngerman]{babel} \usepackage{amsmath} \usepackage{tikz} \usetikzlibrary{plotmarks} \begin{document} \begin{tikzpicture}[ x=3cm, y=3cm, scale=0.75, font=\footnotesize, >=latex, ] % Gitternetzlinien \draw[help lines] (-1.5,-1.5) grid (1.5,1.5); % x-Achse \draw[->] (-1.5,0) -- (1.5,0) node[below] {Re$$}; %Zahlen auf x-Achse \foreach \x in {-1,1,} \draw[shift={(\x,0)},color=black] (0pt,2pt) -- (0pt,-2pt) node[below] {$\x$}; % y-Achse \draw[->] (0,-1.5) -- (0,1.5) node[left] {Im$$};%node[above left] %Zahlen auf y-Achse \foreach \y in {-1,1} \draw[shift={(0,\y)},color=black] (2pt,0pt) -- (-2pt,0pt) node[left] {$\y$}; %Ursprung \node[below left] {$0$}; %%%%%%%%%%%%%%%% %Folge/Dotplot%% %%%%%%%%%%%%%%%% \def\nMin{-99} \def\nMax{-\nMin} \foreach \n in {\nMin,...,\nMax}{%==================== \draw[->,thin] plot[mark=*, mark options={color=red, fill=white}, mark size=1.75pt] coordinates{ ( {cos((4*\n+1)/2 r)},{sin((4*\n+1)/2 r)} ) ( {cos((4*(\n+1)+1)/2 r)},{sin((4*(\n+1)+1)/2 r)} ) }; }%==================== %Titel: \node[red!95!black, align=left] at (1,1.2) {$ \begin{aligned} &z_k = e^{\frac{4k+1}{2}i} \\ & k = \nMin,\dots, \nMax \end{aligned} $}; \end{tikzpicture} \end{document} |
|
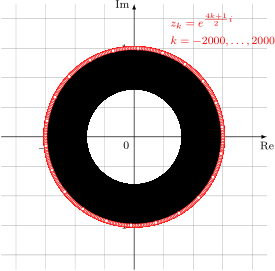
Da stößt der \documentclass{article} \usepackage[ngerman]{babel} \usepackage{amsmath} \usepackage{tikz} \usepackage{xfp} \usetikzlibrary{plotmarks} \begin{document} \begin{tikzpicture}[ x=3cm, y=3cm, scale=0.75, font=\footnotesize, >=latex, ] % Gitternetzlinien \draw[help lines] (-1.5,-1.5) grid (1.5,1.5); % x-Achse \draw[->] (-1.5,0) -- (1.5,0) node[below] {Re}; %Zahlen auf x-Achse \foreach \x in {-1,1,} \draw[shift={(\x,0)},color=black] (0pt,2pt) -- (0pt,-2pt) node[below] {$\x$}; % y-Achse \draw[->] (0,-1.5) -- (0,1.5) node[left] {Im};%node[above left] %Zahlen auf y-Achse \foreach \y in {-1,1} \draw[shift={(0,\y)},color=black] (2pt,0pt) -- (-2pt,0pt) node[left] {$\y$}; %Ursprung \node[below left] {$0$}; %%%%%%%%%%%%%%%% %Folge/Dotplot%% %%%%%%%%%%%%%%%% \def\nMax{2000} \def\nMin{-\nMax} \foreach \n in {\nMin,...,\nMax}{%==================== \draw[->,thin] plot[mark=*, mark options={color=red, fill=white}, mark size=1.75pt] coordinates{ ( \fpeval{cos((4*\n+1)/2)}, \fpeval{sin((4*\n+1)/2)} ) ( \fpeval{cos((4*(\n+1)+1)/2)}, \fpeval{sin((4*(\n+1)+1)/2)} ) }; }%==================== %Titel: \node[red!95!black, align=left] at (1,1.2) {$ \begin{aligned} &z_k = e^{\frac{4k+1}{2}i} \\ & k = \nMin,\dots, \nMax \end{aligned} $}; \end{tikzpicture} \end{document} Braucht allerdings ganz schön lang. Wenn du nicht ganz so lang warten möchtest, dann nimm statt \directlua{ cos = math.cos sin = math.sin } \def\fpeval#1{\directlua{tex.sprint(#1)}}
Ah, sehr gut.
(11 Dez '17, 15:26)
cis
|

Re$$,Im$$? Mich wundert fast, dass da nicht alles in die Luft fliegt.