|
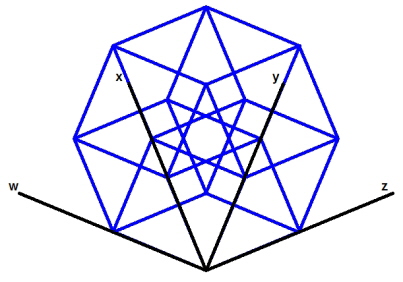
Verwandt mit wie-erstelle-ich-ein-4d-koordinatensystem-in-tikz Ich möchte dieses oder ein ähnliches Bild erzeugen:
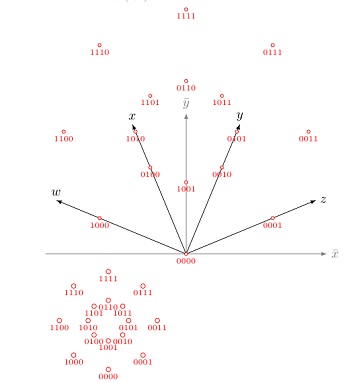
Die Punkte werden in der Schleife von
\documentclass[a4paper]{amsart} \usepackage{selinput} \SelectInputMappings{adieresis={ä}, germandbls={ß}} \usepackage[ngerman]{babel} \usepackage{blindtext} \usepackage{tikz} \usetikzlibrary{calc} \usetikzlibrary{plotmarks} \begin{document} % 4D-Graph ================== \def\beta{22.5} \begin{tikzpicture}[scale=2.5, >=latex, remember picture, ] %4D-Koordinatensystem: \draw[->] (0,0) -- ({1.5*cos(7*\beta)},{1.5*sin(7*\beta)}) node[above]{$w$}; \draw[->] (0,0) -- ({1.5*cos(5*\beta)},{1.5*sin(5*\beta)}) node[above]{$x$}; \draw[->] (0,0) --({1.5*cos(3*\beta)},{1.5*sin(3*\beta)}) node[yshift=2mm]{$y$}; \draw[->] (0,0) -- ({1.5*cos(\beta)},{1.5*sin(\beta)}) node[xshift=2mm]{$z$}; %2D-Zeichenebene \draw[->, gray] (-1.5,0) -- (1.5,0) node[right]{$\bar{x}$}; \draw[->, gray] (0,0) -- (0,1.5) node[above]{$\bar{y}$}; % Hyperwürfel \foreach \w/\x/\y/\z/\Name/\i in {%%% 0/0/0/0/A/1, 0/0/1/0/B/2, 0/1/1/0/C/3, 0/1/0/0/D/4, % 0/0/0/1/E/5, 0/0/1/1/F/6, 0/1/1/1/G/7, 0/1/0/1/H/8, % 1/0/0/0/I/9, 1/0/1/0/J/10, 1/1/1/0/K/11, 1/1/0/0/L/12, % 1/0/0/1/M/13, 1/0/1/1/N/14, 1/1/1/1/O/15, 1/1/0/1/P/16 }%%% % X - Koordinate in Zeichenebene \pgfmathsetmacro{\X}{\w*cos(7*\beta)+\x*cos(5*\beta)+\y*cos(3*\beta)+\z*cos(\beta)} % Y - Koordinate in Zeichenebene \pgfmathsetmacro{\Y}{\w*sin(7*\beta)+\x*sin(5*\beta)+\y*sin(3*\beta)+\z*sin(\beta)} % Punkt zeichnen \draw[thin, color=red, fill=white, ->] plot[mark=*,mark size=0.5pt, only marks] coordinates{ ({\X},{\Y} ) } node[below]{\tiny$\w\x\y\z$}; % \end{tikzpicture} % ======================== \end{document} |
|
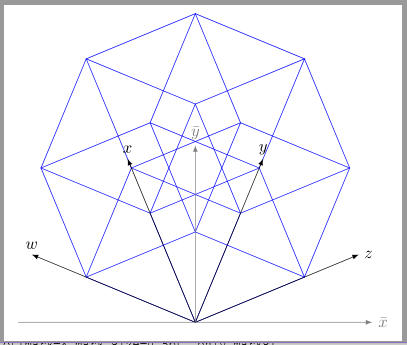
Du kannst in den Eckpunkten Koordinaten setzen und diese systematisch benennen. Da bei Dir alle 4 Koordinaten eines Punktes jeweils nur 0 oder 1 sind, kann man diese dafür nutzen. Danach lassen sich die Koordinaten in einer Schleife verbinden. \documentclass[margin=5pt]{standalone} \usepackage{tikz} \begin{document} \begin{tikzpicture}[scale=2.5, >=latex,graph/.style={blue}] \newcommand*\Beta{22.5} % Hyperwürfel \foreach \w in {0,1} \foreach \x in {0,1} \foreach \y in {0,1} \foreach \z in {0,1} % X - Koordinate in Zeichenebene \pgfmathsetmacro{\X}{\w*cos(7*\Beta)+\x*cos(5*\Beta)+\y*cos(3*\Beta)+\z*cos(\Beta)} % Y - Koordinate in Zeichenebene \pgfmathsetmacro{\Y}{\w*sin(7*\Beta)+\x*sin(5*\Beta)+\y*sin(3*\Beta)+\z*sin(\Beta)} % Koordinate setzen \coordinate(\w\x\y\z) at ({\X},{\Y}); %Kanten zeichnen \foreach \i in {0,1}\foreach \j in {0,1}{ \draw[graph] (0\i\j0)--(0\i\j1)--(1\i\j1)--(1\i\j0)--cycle; \draw[graph] (\i00\j)--(\i10\j)--(\i11\j)--(\i01\j)--cycle; } %4D-Koordinatensystem: \draw[->] (0,0) -- ({1.5*cos(7*\Beta)},{1.5*sin(7*\Beta)}) node[above]{$w$}; \draw[->] (0,0) -- ({1.5*cos(5*\Beta)},{1.5*sin(5*\Beta)}) node[above]{$x$}; \draw[->] (0,0) --({1.5*cos(3*\Beta)},{1.5*sin(3*\Beta)}) node[yshift=2mm]{$y$}; \draw[->] (0,0) -- ({1.5*cos(\Beta)},{1.5*sin(\Beta)}) node[xshift=2mm]{$z$}; %2D-Zeichenebene \draw[->, gray] (-1.5,0) -- (1.5,0) node[right]{$\bar{x}$}; \draw[->, gray] (0,0) -- (0,1.5) node[above]{$\bar{y}$}; \end{tikzpicture} \end{document}
Wow! Sehr stark vereinfacht.
(29 Aug '15, 12:20)
cis
|