|
Hallo Texwelt, möchte ein Rohrsystem bauen. Zwecks 3D-Illusion Rohre schattieren. Mein Versuch war, mit top, bottom, middle color zu arbeiten. Aber wie bei einem Bogen? Gibt es eine Lösung für Nicht-Mathematiker oder hat ein Mathematiker eine Berechnung für die Aussenschattierung eines gebogenen Rohres? Grüße HJ \documentclass[tikz]{standalone} \begin{document} \tikzset{ pics/.cd, % tubeh tubeh/.style={ code={ \draw[top color=green, bottom color=green, middle color=white] (0,0) rectangle +(2,1); }%end code }%end style }%end tikzset \tikzset{ pics/.cd, % tubev tubev/.style={ code={ \draw[left color=green, right color=green, middle color=white] (0,0) rectangle +(1,2); }%end code }%end style }%end tikzset \tikzset{ pics/.cd, % tubearc tubearc/.style={ code={ % means 1cm in direction 0 degree \draw[top color=green, bottom color=green, middle color=white] (0:1cm) -- (0:2cm) % draw arc: start angle, end angle, radius arc (0:90:2cm) -- (90:1cm) arc (90:0:1cm) -- cycle; }%end code }%end style }%end tikzset \begin{tikzpicture}% \draw[step=1, help lines](-2,-2) grid (5,2); \foreach \x in {-2,...,5} \draw (\x cm,1pt) -- (\x cm,-1pt) node[anchor=north] {$\x$}; \foreach \y in {-2,...,2} \draw (1pt,\y cm) -- (-1pt,\y cm) node[anchor=east] {$\y$}; \path (-2,1) pic {tubeh} (0.0,0.0) pic {tubearc} (1,-2) pic {tubev}; \end{tikzpicture} \end{document}
|
|
Hier ist ein Vorschlag. \documentclass[tikz]{standalone} \begin{document} \tikzset{ pics/.cd, % tubeh tubeh/.style={ code={ \draw[top color=green, bottom color=green, middle color=white] (0,0) rectangle +(2,1); }%end code }%end style }%end tikzset \tikzset{ pics/.cd, % tubev tubev/.style={ code={ \draw[left color=green, right color=green, middle color=white] (0,0) rectangle +(1,2); }%end code }%end style }%end tikzset \tikzset{ pics/.cd, % tubearc tubearc/.style={ code={ % means 1cm in direction 0 degree \draw[clip] (0:1cm) -- (0:2cm) % draw arc: start angle, end angle, radius arc (0:90:2cm) -- (90:1cm) arc (90:0:1cm) -- cycle; \foreach \X in {0,5,...,85} % <- Du kannst die Stufen hier feiner waehlen {\shade[left color=green, right color=green, middle color=white,transform canvas={rotate=\X}] (0:1cm) -- (0:2cm) arc (0:{5}:2cm) -- ({5}:1cm) arc ({5}:{0}:1cm) -- cycle;} }%end code }%end style }%end tikzset \begin{tikzpicture}% \draw[step=1, help lines](-2,-2) grid (5,2); \foreach \x in {-2,...,5} \draw (\x cm,1pt) -- (\x cm,-1pt) node[anchor=north] {$\x$}; \foreach \y in {-2,...,2} \draw (1pt,\y cm) -- (-1pt,\y cm) node[anchor=east] {$\y$}; \path (-2,1) pic {tubeh} (0.0,0.0) pic {tubearc} (1,-2) pic {tubev}; \end{tikzpicture} \end{document} Wenn Du super genau reinzoomen magst, kannst Du die Stufen feiner machen, die Stelle ist im Code markiert. 1
@Murmeltier Du hast ja bereits eine Vielzahl toller TikZ-Beispiele geschaffen. Hast Du evtl. Lust, die schönsten und lehrreichen Beispiele auf TeXample.net in die Galerie zu stellen? (Ist etwas Arbeit: Auswahl, Tags zuordnen, etwas kommentieren. Technisch in die Galerie einpflegen würde ich tun.) Bei Interesse schick mir gern eine mail an stefan@latex.org
(27 Aug '18, 15:43)
stefan ♦♦
|

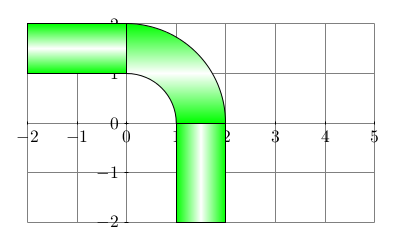
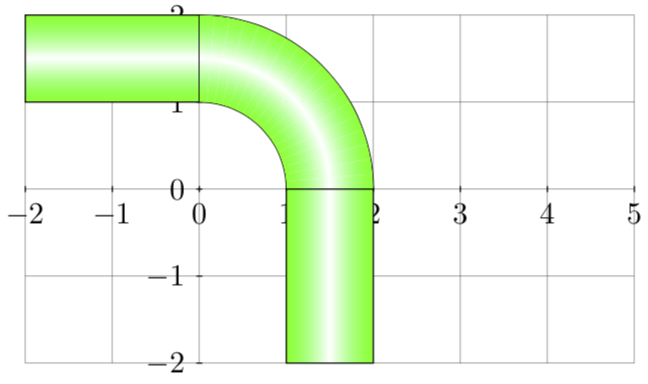
Idee: was rund aussieht ist im Polarkoordinatensystem gerade - dort schattieren (wenn es geht). Weitere, vmtl. besser ;-) Idee: normal linear schattieren, doch dann eine Koordinatentransformation anwenden, die das ursprünglich gerade Rohrstück auf so ein Eckstück "biegt", und damit auch die Schattierung.
@stefan: Danke für deine Antwort. normal linear schattieren. Code-Schnipsel wäre super. Ein Beispiel wäre super, denn Koordinatentransformation kann ich noch nicht.
http://tex.stackexchange.com/questions/286655/shading-bent-tube
@stefan Leider sind die Schattierungen immun gegen normale, d.h. nicht rabiate, Koordinatentransformationen. Zu diesen zählen auch die nichtlinearen. Allerdings kannst Du Schattierungen durch canvas transformations (Segeltuchtransformationen klingt bescheuert;-) transformieren, jedoch sind mir bisher noch keine nichtlinearen canvas Transformationen über den Weg gelaufen. Wenn man die aber durch stückweise lineare Transformationen approximiert, geht Dein Plan (den ich erst jetzt lese) genau auf.