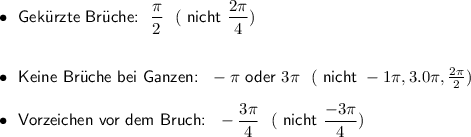|
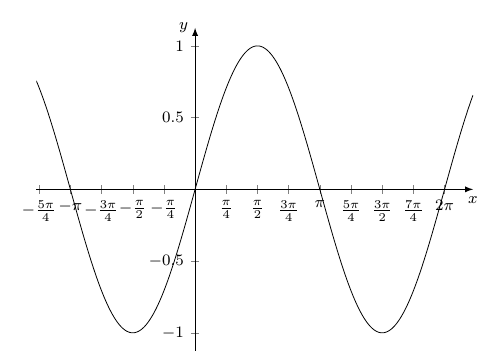
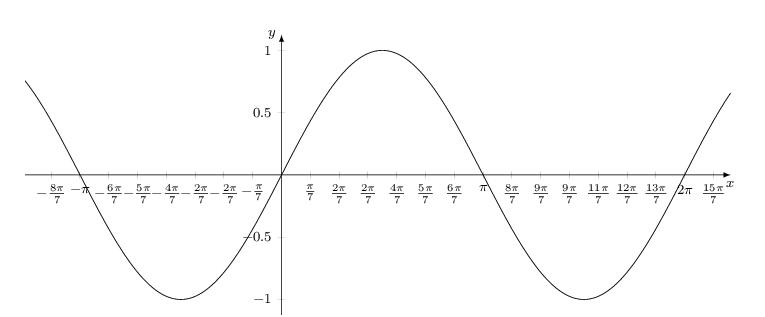
Die Frage ist zum Archivieren gedacht, kein Support benötigt. Antworten sind jedoch gern gesehen und sehr willkommen! Ich beantworte die Frage auch selbst. Etwa bei trigonometrischen Kurven wünscht man oft eine Achsenskalierung mit Pi-Faktoren. Meistens werden Pi-Ganze, Pi-Halbe oder Pi-Viertel Unterteilungen gewählt, das heißt "Unterteilungstiefe" 1 bzw. 2 bzw. 4. Günstig wäre also ein Code, der eine beliebige Unterteilungstiefe erlaubt (also z.B. auch Skalierung mit Pi-Siebtel Faktoren) und dabei folgenden Darstellungskriterien genügt: Wie kann man das umsetzen? |
|
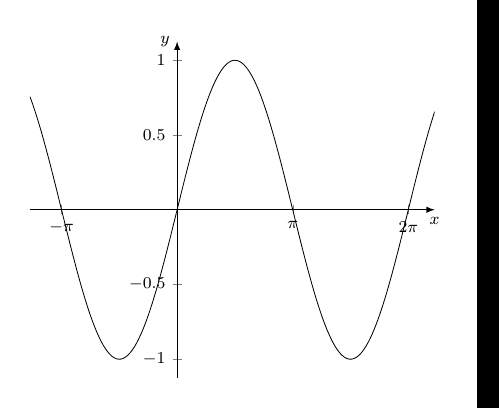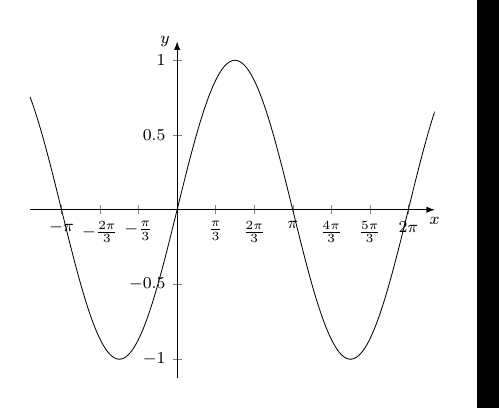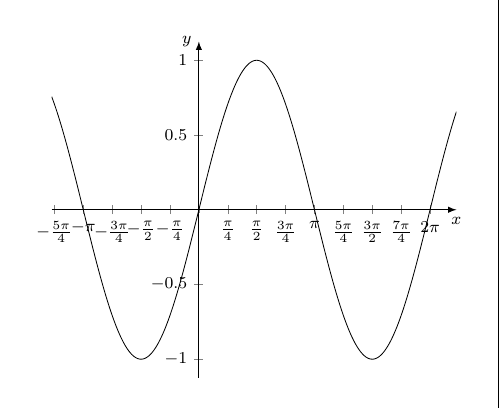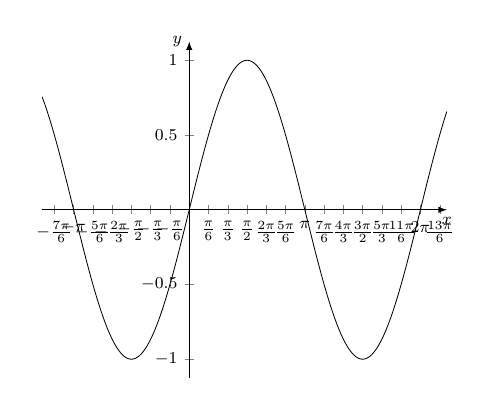
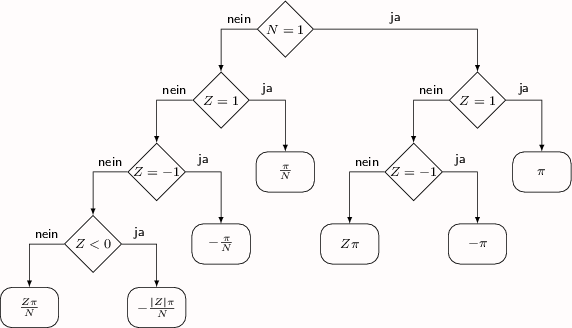
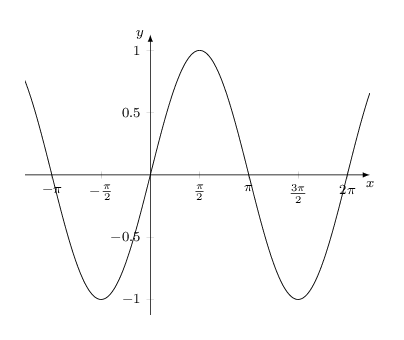
Zunächst benötigt man eine Liste mit Werten (z.B. -pi, -3pi/4,..., 3pi) % Liste mit tick-Werten erstellen \pgfmathsetmacro{\pinum}{3.142} % Rechengenauigkeit \pgfmathtruncatemacro{\u}{4} % Unterteilungstiefe % Reichweite der Ticks festlegen \def\Range{-20,...,20} % xticklist erstellen \newcommand{\xticklist}{}% Name reservieren \let\xticklist=\empty% Liste erstellen \makeatletter \foreach \n in \Range { \pgfmathparse{\n*\pinum/\u}% \ifx\empty\xticklist{} \protected@xdef\xticklist{\pgfmathresult}% \else \protected@xdef\xticklist{\xticklist,\pgfmathresult}% \fi }\makeatother Anzeigen: \xticklist Für die gewünschten Darstellungskriterien kann man, im Hinblick auf Zähler (Z) und Nenner (N) des Pi-Faktorenbruches, folgendes Ablaufdiagramm verwenden: das setzt xtick/.expanded = {\xticklist}, xticklabel={% \pgfmathsetmacro{\p}{int(\tick*\u/\pinum)}% pi-Faktor \pgfmathsetmacro{\Z}{int(\p/gcd(\p,\u))}% Zähler \pgfmathsetmacro{\Zabs}{int(abs(\Z))}% Zähler-Betrag \pgfmathsetmacro{\N}{int(\u/gcd(\p,\u))}% Nenner \pgfmathparse{% \N == 1 ? (\Z==1 ? "\pi" : (\Z==-1 ? "-\pi" : "\Z\pi")) :% (\Z==1 ? "\frac{\pi}{\N}" : (\Z==-1 ? "-\frac{\pi}{\N}" :% (\Z<0 ? "-\frac{\Zabs\pi}{\N}" : "\frac{\Z\pi}{\N}")% ))% } $\pgfmathresult$% %$\frac{\Z}{\N}$% zum Testen }, Kleiner Warnhinweis: Die Rechengenauigkeit von pgfmath ist nicht beliebig; z.B. ab Pi-Neuntel Unterteilung kommen Fehler rein. Im Ergebnis Beispiel 1: \pgfmathtruncatemacro{\u}{2} % Unterteilungstiefe Beispiel 2: \pgfmathtruncatemacro{\u}{7} % Unterteilungstiefe Ganzer Code: %\documentclass[]{article} \documentclass[border=5mm, tikz]{standalone} \usepackage{pgfplots} \pgfplotsset{compat=1.13} \begin{document} % Eingaben \pgfmathsetmacro{\xStauchung}{0.58500055}% Stauchung x-Achse % Liste mit tick-Werten erstellen \pgfmathsetmacro{\pinum}{3.142} % Rechengenauigkeit \pgfmathtruncatemacro{\u}{7} % Unterteilungstiefe % Reichweite der Ticks festlegen \def\Range{-20,...,20} % xticklist erstellen \newcommand{\xticklist}{}% Name reservieren \let\xticklist=\empty% Liste erstellen \makeatletter \foreach \n in \Range { \pgfmathparse{\n*\pinum/\u}% \ifx\empty\xticklist{} \protected@xdef\xticklist{\pgfmathresult}% \else \protected@xdef\xticklist{\xticklist,\pgfmathresult}% \fi }\makeatother %Anzeigen: \xticklist % Zeichnen \pgfmathsetmacro{\xScale}{\xStauchung*\u/pi}% \begin{tikzpicture}[] \begin{axis}[ font=\footnotesize, x = \xScale cm, %y = 1cm, axis lines=middle, xlabel=$x$,xlabel style={anchor=north}, ylabel=$y$,ylabel style={anchor=east}, x axis line style = {-latex}, y axis line style = {-latex}, % xtick/.expanded = {\xticklist}, xticklabel={% \pgfmathsetmacro{\p}{int(\tick*\u/\pinum)}% pi-Faktor \pgfmathsetmacro{\Z}{int(\p/gcd(\p,\u))}% Zähler \pgfmathsetmacro{\Zabs}{int(abs(\Z))}% Zähler-Betrag \pgfmathsetmacro{\N}{int(\u/gcd(\p,\u))}% Nenner \pgfmathparse{% \N == 1 ? (\Z==1 ? "\pi" : (\Z==-1 ? "-\pi" : "\Z\pi")) :% (\Z==1 ? "\frac{\pi}{\N}" : (\Z==-1 ? "-\frac{\pi}{\N}" :% (\Z<0 ? "-\frac{\Zabs\pi}{\N}" : "\frac{\Z\pi}{\N}")% ))% } $\pgfmathresult$% %$\frac{\Z}{\N}$% zum Testen }, minor xtick/.expanded = {\xticklist}, % enlarge y limits={abs=0.125}, % kein Effekt ] \addplot[domain=-4:7, samples=300] {sin(deg(x))}; \end{axis} \end{tikzpicture} \end{document} Code für das Ablaufdiagramm: \documentclass[border=5pt]{standalone} \usepackage{selinput} \SelectInputMappings{adieresis={ä},germandbls={ß}} \usepackage{tikz} \usetikzlibrary{matrix,shapes} \tikzset{% treenode/.style = {%fill=gray!10, shape=rectangle, draw, anchor=center, %text width=5em, align=center, %draw=cyan, very thick, text=black, text width=1cm, %inner sep=1ex }, startstop/.style = {treenode, rounded corners=7pt}, process/.style = {treenode}, decision/.style = {treenode, diamond, inner sep=0pt}, output/.style={treenode, trapezium,trapezium left angle=60, trapezium right angle=120, font=\sffamily\slshape\tiny}, input/.style={treenode, trapezium,trapezium left angle=120, trapezium right angle=60}, predefprocess/.style = {treenode, path picture={\draw[treenode, -] ([xshift=1mm]path picture bounding box.north west)--([xshift=1mm]path picture bounding box.south west) ([xshift=-1mm]path picture bounding box.north east)--([xshift=-1mm]path picture bounding box.south east);}}, }% \newcommand{\ja}{-| node [auto=left, near start] {ja}} \newcommand{\nein}{-| node [auto=right, near start] {nein}} \begin{document} \begin{tikzpicture}[scale=0.5, font=\sffamily\tiny, >=latex, ->, %every path/.style={red, very thick}, ] %\pgfgettransform\mytrafo \def\Start{|[decision]| N=1} \def\ZEins{|[decision]| Z = 1} \def\ZnegEins{|[decision]| Z = -1} \def\Zneg{|[decision]| Z < 0} \def\ZposI{|[startstop, minimum height=0.85cm]| \frac{Z\pi}{N}} \def\ZposII{|[startstop, minimum height=0.85cm]| -\frac{|Z|\pi}{N}} \def\ZposEins{|[startstop, minimum height=0.85cm]| \frac{\pi}{N}} \def\ZnegEinsI{|[startstop, minimum height=0.85cm]| -\frac{\pi}{N}} \def\ZposIII{|[startstop, minimum height=0.85cm]| Z\pi} \def\ZposIV{|[startstop, minimum height=0.85cm]| -\pi} \def\ZNEins{|[startstop, minimum height=0.85cm]| \pi} \matrix (m) [ %execute at begin cell=\pgfsettransform\mytrafo, matrix of math nodes, nodes in empty cells, column sep =0.75ex, row sep = 2ex, %nodes={process}, % default %column 1/.style = {nodes={decision}}, %column 2/.style = {nodes={process}} ] { %1 & 2 & 3 & 4 & 5 & \Start & 7 & 8 & 9 & 10 \\ & & & & & \Start & & & & \\ & & & & \ZEins & & & & \ZEins & \\ & & &\ZnegEins & & \ZposEins & & \ZnegEins & & \ZNEins \\ & & \Zneg & & \ZnegEinsI & & \ZposIII & & \ZposIV & \\ & \ZposI & & \ZposII & & & & & & \\ %1& 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ }; % Links \draw[] (m-1-6) \nein (m-2-5); \draw[] (m-2-5) \nein (m-3-4); \draw[] (m-2-5) \ja (m-3-6); \draw[] (m-3-4) \nein (m-4-3); \draw[] (m-3-4) \ja (m-4-5); \draw[] (m-4-3) \nein (m-5-2); \draw[] (m-4-3) \ja (m-5-4); % Rechts \draw[] (m-1-6) \ja (m-2-9); \draw[] (m-2-9) \nein (m-3-8); \draw[] (m-2-9) \ja (m-3-10); \draw[] (m-3-8) \nein (m-4-7); \draw[] (m-3-8) \ja (m-4-9); \end{tikzpicture} \end{document} |