|
Hi liebe LaTeX-Freunde, ich bin ein ziemlicher Neuling was den Umgang mit LaTeX betrifft und stehe vor dem Problem, dass ich eine Ellipse der Form:
plotten möchte, wobei a eine reelle Konstante sein soll und b verschiedene natürliche Zahlen annehmen (sprich die Ellipse in unterschiedlichen Größen in einem Koordinatensystem dargestellt sein soll, z.B. b=1,2,3,...).
Ich habe verstanden, wie ich mit den TikZ und Viele Grüße
Ross |
RechnenOhne ein wenig zu rechnen, geht es wahrscheinlich nicht. Du kannst deine implizite Gleichung nach
Bedeutung
CodeDie wahrscheinlich beste Variante ist, in Polarkoordinaten zu transformieren und dann mit Beispiel
VerallgemeinerungMan kann die Formel verallgemeinern zu
Welche Variable dabei welche Bedeutung zukommt überlasse ich dem geneigten Leser ;-) Perfekt! Danke! Damit kann ich arbeiten!
(18 Dez '13, 11:05)
Ross
|
|
Da hier a und b, also die Halbachsen bekannt sind, ein solches Beispiel mit pgfplots, aus dem Handbuch:
Nur wie komme ich von a und b aus obiger Gleichung auf die Halbachsen und den Rotations-Winkel?
(16 Dez '13, 17:29)
Ross
Etwas Mathematik, sieheEllipse in der Wikipedia, a und b stehen dort in der Mittelpunktgleichung, Deine implizite Form ist weiter unten genannt. Das könnte man umrechnen (multipliziere mal implizite Gleichung mit a^2 b^2).
(16 Dez '13, 18:35)
stefan ♦♦
Irgendwie schein ich mich gerade ganz dumm anzustellen, aber ich finde meine implizite Form in dem Wikipedia Artikel nirgends, lediglich die Form x^2/a^2+y^2/b^2=1, wie ich diese Form allerdings auf x^2+cxy+y^2=d umformen kann erschließt sich mir leider noch nicht so ganz :/
(17 Dez '13, 08:12)
Ross
|


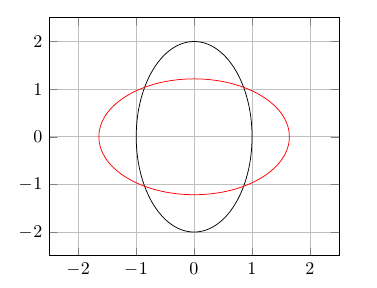
Weitere Ideen:
raw gnuplotmit Tikz, und\psplotImpmit PSTricks, evtl. hat jemand Zeit dafür, das zu testen (ich im Augenblick noch nicht).