|
Folgendes Programm liefert ab ! Arithmetic overflow. \pgfmath@iterate ...pgfmath@x by\c@pgfmath@counta \advance \c@pgfmath@counta... Gibt es eine einfache Möglichkeit, das zu fixen?
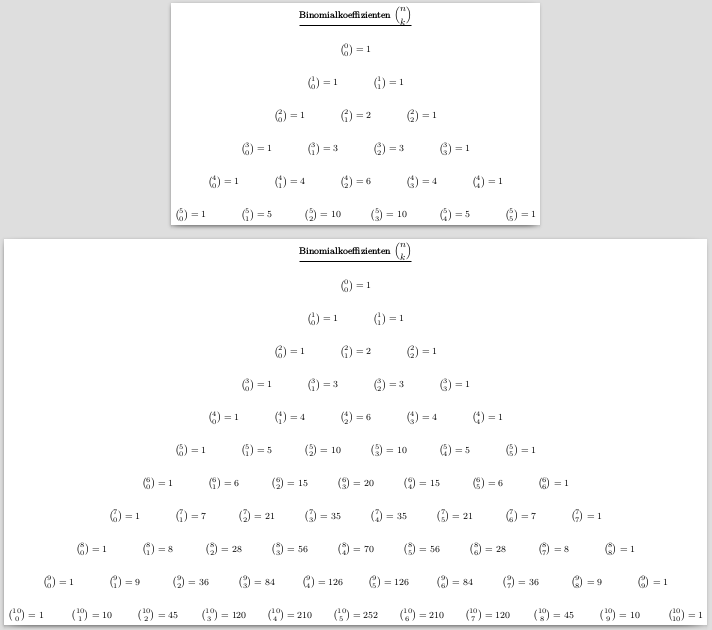
\documentclass[margin=30mm, varwidth]{standalone} %\documentclass{article} \usepackage{amsmath} \usepackage{tikz} % \usetikzlibrary{positioning} \begin{document} \pagecolor{yellow!65} \begin{tikzpicture}[%scale=2.0,transform shape, font=\footnotesize, declare function={BinCoeff(\k,\n)=\n!/(\k!*(\n-\k)!);}, ] % Binomialkoeffizienten \foreach \n in {0,...,7} {%----------------------------------------- \foreach \k in {0,...,\n} {%% \pgfmathtruncatemacro\myresult{BinCoeff(\k,\n)} % % Ausführliches Ergebnis \node[align=center](\n) at (2*\k-1*\n,-\n) { $\binom{\n}{\k} = \myresult$ }; % % Kurzes Ergebnis %\node(\n) at (\k-\n/2,-\n) {$\myresult$}; % }%% }%----------------------------------------- \node[above of = 0]{\underline{Binomialkoeffizienten $\dbinom{n}{k}$}}; \end{tikzpicture} \end{document} |
|
Man kann den im zweiten Beispiel meiner \documentclass[margin=2mm]{standalone} %\documentclass{article} \usepackage{amsmath} \usepackage{tikz} % \usetikzlibrary{positioning} \makeatletter \newcommand{\binomial}[2]{% \ifnum #2=0 % \typeout{binomial(#1,#2)=1}% 1% \else \ifnum \numexpr 2*#2\relax>#1 \binomial{#1}{\the\numexpr #1-#2\relax}% \else \@tempcnta=\numexpr #1 - #2 + 1\relax \@tempcntb=1 \@whilenum \@tempcntb<#2 \do {% \advance\@tempcntb by 1 \@tempcnta=\numexpr \@tempcnta * (#1 - #2 + \@tempcntb)\relax \@tempcnta=\numexpr \@tempcnta / \@tempcntb }% % \typeout{binomial(#1,#2)=\the\@tempcnta}% \the\@tempcnta \fi \fi } \begin{document} \pagecolor{yellow!65} \begin{tikzpicture}[%scale=2.0,transform shape, font=\footnotesize, ] % Binomialkoeffizienten \foreach \n in {0,...,20} {%----------------------------------------- \foreach \k in {0,...,\n} {% % Ausführliches Ergebnis \node[align=center](\n) at (2*\k-1*\n,-\n) { $\binom{\n}{\k} = \binomial{\n}{\k}$ }; % % Kurzes Ergebnis % \node(\n) at (\k-\n/2,-\n) {$\binomial{\n}{\k}$}; % }%% }%----------------------------------------- \node[above of = 0]{\underline{Binomialkoeffizienten $\dbinom{n}{k}$}}; \end{tikzpicture} \end{document}
Wer die ganzen Low-Level-(La)TeX-Bedingungen, -Scheifen und LaTeX-internen TeX-Zähler nicht mag, kann dafür auch das Paket \documentclass[margin=2mm]{standalone} %\documentclass{article} \usepackage{amsmath} \usepackage{tikz} % \usetikzlibrary{positioning} \usepackage{ifthen} \newcounter{binomiali}% Schleifenzähler \newcounter{binomialresult}% Zwischen- und Endergebnis \newcommand{\binomial}[2]{% \ifthenelse{#2=0}{% % \typeout{binomial(#1,#2)=1}% 1% }{% \ifthenelse{\numexpr 2*#2\relax>#1}{% \binomial{#1}{\the\numexpr #1-#2\relax}% }{% \setcounter{binomialresult}{\numexpr #1 - #2 + 1}% \setcounter{binomiali}{1}% \whiledo{\value{binomiali}<#2}{% \stepcounter{binomiali}% \setcounter{binomialresult}{% \numexpr \value{binomialresult} * (#1 - #2 + \value{binomiali})% } \setcounter{binomialresult}{% \numexpr \value{binomialresult}/\value{binomiali}% } }% % \typeout{binomial(#1,#2)=\thebinomialresult}% \thebinomialresult }% }% } \begin{document} \pagecolor{yellow!65} \begin{tikzpicture}[%scale=2.0,transform shape, font=\footnotesize, ] % Binomialkoeffizienten \foreach \n in {0,...,10} {%----------------------------------------- \foreach \k in {0,...,\n} {% % Ausführliches Ergebnis \node[align=center](\n) at (2*\k-1*\n,-\n) { $\binom{\n}{\k} = \binomial{\n}{\k}$ }; % % Kurzes Ergebnis % \node(\n) at (\k-\n/2,-\n) {$\binomial{\n}{\k}$}; % }%% }%----------------------------------------- \node[above of = 0]{\underline{Binomialkoeffizienten $\dbinom{n}{k}$}}; \end{tikzpicture} \end{document} Wie zu sehen ist, kommt man mit diesem Algorithmus deutlich weiter als bis n=7. Bei 29 ist mit dieser Lösung allerdings Schluss, während die Ich selbst empfehle übrigens eher die Ahhhjaaa... Alles nicht ganz einfach :) Ich hatte auf sowas wie
(01 Okt '15, 08:53)
cis
Was ich tatsächlich gerne hätte, wäre eine
(01 Okt '15, 09:11)
saputello
|
|
Dann will ich auch noch meinen Lua-Senf dazugeben. Für mich ist die Anwemdung von LuaLaTeX die einzig sinnvolle Alternative: \documentclass[10pt,tikz]{standalone} \usepackage{amsmath} \usepackage{fontspec} \def\BinCoeff(#1,#2){% (k,n) \directlua{ local k, n =#1, #2 if k > n/2 then k = n - k end local numer, denom = 1, 1 for i = 1, k do numer = numer * ( n - i + 1 ) denom = denom * i end tex.print(numer/denom) }} \def\Dreieck#1{% \begin{tikzpicture}[font=\footnotesize] \foreach \n in {0,...,#1} {% \foreach \k in {0,...,\n}{%% \node[align=center](\n) at (2*\k-1*\n,-\n) {% $\binom{\n}{\k} = \BinCoeff(\k,\n)$}; }}% \node[above of = 0]{\underline{Binomialkoeffizienten $\dbinom{n}{k}$}}; \end{tikzpicture}} \begin{document} \Dreieck{5}\par \Dreieck{10} \end{document}
|
|
Für große Zahlen bietet es sich an, Berechnungen mit Lua zu machen (setzt natürlich die Verwendung von \documentclass[margin=30mm]{standalone} %\documentclass{article} \usepackage{amsmath} \usepackage{tikz} % \usetikzlibrary{positioning} \usepackage{luacode} \begin{luacode} function factorial (n) if (n == 0) then return 1 else return n*factorial(n-1) end end function binomial (n,k) return factorial(n)/(factorial(k)*factorial(n-k)) end \end{luacode} \newcommand{\binomial}[2]{% \directlua{tex.print ( binomial ( #1, #2 ) ) } } \begin{document} \pagecolor{yellow!65} \begin{tikzpicture}[%scale=2.0,transform shape, font=\footnotesize, ] % Binomialkoeffizienten \foreach \n in {0,...,10} {%----------------------------------------- \foreach \k in {0,...,\n} {% % Ausführliches Ergebnis \node[align=center](\n) at (2*\k-1*\n,-\n) { $\binom{\n}{\k} = \binomial{\n}{\k}$ }; % % Kurzes Ergebnis % \node(\n) at (\k-\n/2,-\n) {$\binomial{\n}{\k}$}; % }%% }%----------------------------------------- \node[above of = 0]{\underline{Binomialkoeffizienten $\dbinom{n}{k}$}}; \end{tikzpicture} \end{document}
Die Rechenfähigkeiten von Lua sind weit besser als die von TeX. Übrigens ist die Formel mit den Fakultäten eine sehr ineffektive Methode zur Berechnung von Binomialkoeffizienten. Die Umsetzung der Produktformel als Algorithmus (egal ob als Schleife oder Rekursion) ist dagegen wesentlich effizienter, weil dabei keine riesigen Zwischenergebnisse wie n! oder k! entstehen, die sehr schnell zu Überläufen führen. Im mit Deiner Grafik noch darstellbaren Bereich bis ca. 25 ist die Fakultätsformel in Lua aber kein Problem, weshalb ich sie beibehalten habe. Spaßeshalber habe ich es sogar mit n=100 durchlaufen lassen, was zwar zu Darstellungsproblemen führt, die Berechnung selbst funktioniert aber sogar in erträglicher Zeit (weniger als eine Minute auf meinem langsamen Notebook). Aus Lust und Laune hier trotzdem eine für größere n effizientere Lösung: \documentclass[margin=2mm]{standalone} %\documentclass{article} \usepackage{amsmath} \usepackage{tikz} % \usetikzlibrary{positioning} \usepackage{luacode} \begin{luacode} function binomial (n,k) if (k == 0) then return 1 else if (2*k > n) then return binomial (n, n-k) else b = n - k + 1 for i=2,k,1 do b = b * (n - k + i) b = b / i end return b end end end \end{luacode} \newcommand{\binomial}[2]{% \directlua{tex.print ( binomial ( #1, #2 ) ) } } \begin{document} \pagecolor{yellow!65} \begin{tikzpicture}[%scale=2.0,transform shape, font=\footnotesize, ] % Binomialkoeffizienten \foreach \n in {0,...,10} {%----------------------------------------- \foreach \k in {0,...,\n} {% % Ausführliches Ergebnis \node[align=center](\n) at (2*\k-1*\n,-\n) { $\binom{\n}{\k} = \binomial{\n}{\k}$ }; % % Kurzes Ergebnis % \node(\n) at (\k-\n/2,-\n) {$\binomial{\n}{\k}$}; % }%% }%----------------------------------------- \node[above of = 0]{\underline{Binomialkoeffizienten $\dbinom{n}{k}$}}; \end{tikzpicture} \end{document} Aja, gut.
(30 Sep '15, 22:38)
cis
(01 Okt '15, 07:31)
saputello
|