|
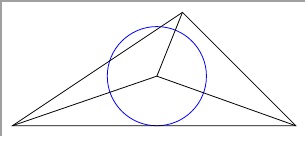
Ich habe die Koordinaten nach diesen Angaben berechnet; allerdings erhalte ich dieses Ergebnis:
Daher vermute ich, dass mit dem Inkreismittelpunkt W etwas nicht stimmt. Könnte es an Rechenungenauigkeit liegen? \documentclass[border=5pt, varwidth]{standalone} %\documentclass[]{article} \usepackage[utf8]{inputenc} \usepackage[ngerman]{babel} \usepackage[T1]{fontenc} \usepackage{amsmath,amsfonts,amssymb} \usepackage{tikz} % \usetikzlibrary{calc} \begin{document} \begin{tikzpicture}[scale=1] % Koordinaten der Eckpunkte \def\xA{0} \def\yA{0} \def\xB{5} \def\yB{0} \def\xC{3} \def\yC{2} \coordinate (A) at (\xA,\yA); \coordinate (B) at (\xB,\yB); \coordinate (C) at (\xC,\yC); % Seitenlängen \pgfmathsetmacro{\a}{sqrt((\xA - \xC)^2 + (\yA - \yC)^2)} \pgfmathsetmacro{\b}{sqrt((\xB - \xC)^2 + (\yB - \yC)^2)} \pgfmathsetmacro{\c}{sqrt((\xA - \xB)^2 + (\yA - \yB)^2)} % Inkreis % Koordinate des Inkreismittelpunktes \pgfmathsetmacro{\P}{\a+\b+\c} \pgfmathsetmacro{\xW}{(\a*\xA + \b*\xB + \c*\xC)/\P} \pgfmathsetmacro{\yW}{(\a*\yA + \b*\yB + \c*\yC)/\P} \coordinate (W) at (\xW,\yW); % Inkreisradius \pgfmathsetmacro{\s}{\P/2} \pgfmathsetmacro{\r}{sqrt(((\s-\a)*(\s-\b)*(\s-\c))/\s)} % Inkreis zeichnen \draw[blue] (W) circle[radius=\r]; % Winkelhalbierende \draw (W) -- (A); \draw (W) -- (B); \draw (W) -- (C); \draw[] (A) -- (B) -- (C) -- cycle; \end{tikzpicture} \end{document} |
|
Dir ist ein kleiner semantischer Fehler bei den Definitionen der Seitenlängen unterlaufen. Die Seite a wird durch die Punkte B und C gebildet und nicht durch A und C, wie bei dir. Ersetze % Seitenlängen \pgfmathsetmacro{\a}{sqrt((\xA - \xC)^2 + (\yA - \yC)^2)} \pgfmathsetmacro{\b}{sqrt((\xB - \xC)^2 + (\yB - \yC)^2)} \pgfmathsetmacro{\c}{sqrt((\xA - \xB)^2 + (\yA - \yB)^2)} durch % Seitenlängen \pgfmathsetmacro{\b}{sqrt((\xA - \xC)^2 + (\yA - \yC)^2)} \pgfmathsetmacro{\a}{sqrt((\xB - \xC)^2 + (\yB - \yC)^2)} \pgfmathsetmacro{\c}{sqrt((\xA - \xB)^2 + (\yA - \yB)^2)} und es funktioniert. Als Alternative mit tkz-euclide \documentclass[border=5pt, varwidth]{standalone} \usepackage[utf8]{inputenc} \usepackage[ngerman]{babel} \usepackage[T1]{fontenc} \usepackage{amsmath,amsfonts,amssymb} \usepackage{tkz-euclide} \usetkzobj{all} \begin{document} \begin{tikzpicture}[scale=1] % Koordinaten der Eckpunkte \tkzDefPoint(0,0){A} \tkzDefPoint(5,0){B} \tkzDefPoint(3,2){C} \tkzDrawPoints(A,B,C) \tkzDrawSegments(A,B B,C C,A) % Inkreis % Koordinate des Inkreismittelpunktes \tkzDefCircle[in](A,B,C) \tkzGetPoint{W} % Inkreisradius \tkzGetLength{rIN} % Inkreis zeichnen \tkzDrawCircle[R,blue](W,\rIN pt) % Winkelhalbierende \tkzDrawSegments(A,W B,W C,W) \end{tikzpicture} \end{document} Greets Marcel Upps, wie peinlich. Danke Dir. PS: tkz-euclide wollte ich jetzt nicht verwenden, aber mit der Ersetzung geht es auch in meinem Code.
(20 Jun '16, 18:11)
cis
Kein Problem, man verliert ja schnell den Überblick. @cis Hat es einen bestimmten Grund tkz-euclide nicht zu verwenden (ohne jetzt eine große Diskussion starten zu wollen)?
(20 Jun '16, 18:18)
maphy-psd
Ich wollte möglichst elementar bleiben; ich finde das -trotz umfangreicheren Code- oft auch besser zum Nachvollziehen.
(20 Jun '16, 19:06)
cis
|