|
Zu meiner Frage nach einem Kreis durch einen bestimmten Punkt, wo das Zentrum bekannt war, gab es ja eine elegante Lösung mit der Nun möchte ich nun einen Kreisbogen zwischen zwei vorgegebenen Punkten zeichnen, also von einem Punkt zum nächsten, mit vorgegebenem Radius. Wie kann man das machen? Im Handbuch fand ich die |
|
|
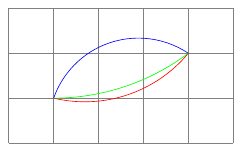
Hier noch eine einfache
Kurzfristiger Vorteil dieser Lösung ist allerdings, dass es den allseits bekannten Eigentlich, denn mit der CVS-Version wird der Bogen statt zum relativen Punkt Code (2.10)Output (2.10)
Code (2.10-CVS)Output (2.10-CVS)
Die im letzten Absatz erwähnte notwendige Korrektur an der Berechnung der Winkel wurde notwendig, da die Reihefolge der Argumente zur Man mag über diese Änderungen denken, was man will; die einfachste Lösung ist wohl die direkte Verwendung von
(08 Dez '13, 05:38)
Qrrbrbirlbel
@Qrrbrbirlbel heißt dass, ein Update von pgf auf CTAN steht vor der Tür?
(08 Dez '13, 10:16)
cgnieder
@Clemens Ich weiß das nicht, ich arbeite ja nicht an PGF/TikZ. Und ich weiß auch nicht, warum du darauf kommst. Allerdings hat Christian Feuersänger in einem Kommentar zu einer anderen Frage von „demnächst voraussichtlich“ gesprochen. Irgendwo auf der SourceForge-Seite von PGF gibt es auch ein Link zum Manual der nächsten Version, das bereits mit der Versionsnummber 3.0.0 versehen ist. Eventuell ein weiteres Indiz, dass ein Release bald zu erwarten ist?
(08 Dez '13, 21:22)
Qrrbrbirlbel
@Qrrbrbirlbel weil Du die Änderung von
(08 Dez '13, 21:52)
cgnieder
|
|
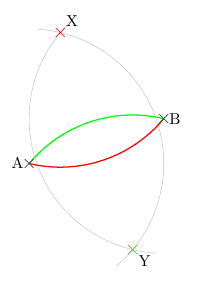
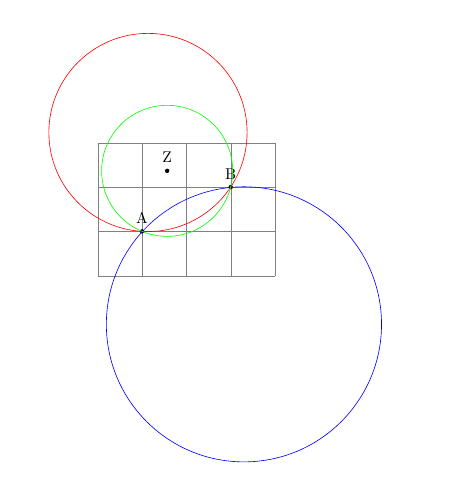
Meine ursprüngliche Antwort berechnet den Radius falsch aufgrund eines Denkfehlers meinerseits. Wo der Fehler passiert, bleibt dem Leser als Aufgabe überlassen. Da @QrrBrBirlbel in seiner Antwort mit einer neuen TikZ-Erweiterung schon die vermutlich beste TikZ-Antwort gegeben hat, nehme ich die Gelegenheit wahr, ein TikZ-Paket zu verwenden, das schon lange in meinem Hinterkopf spukte, mit dem ich mich aber erst seit kurzem näher beschäftige: Alain Matthes'
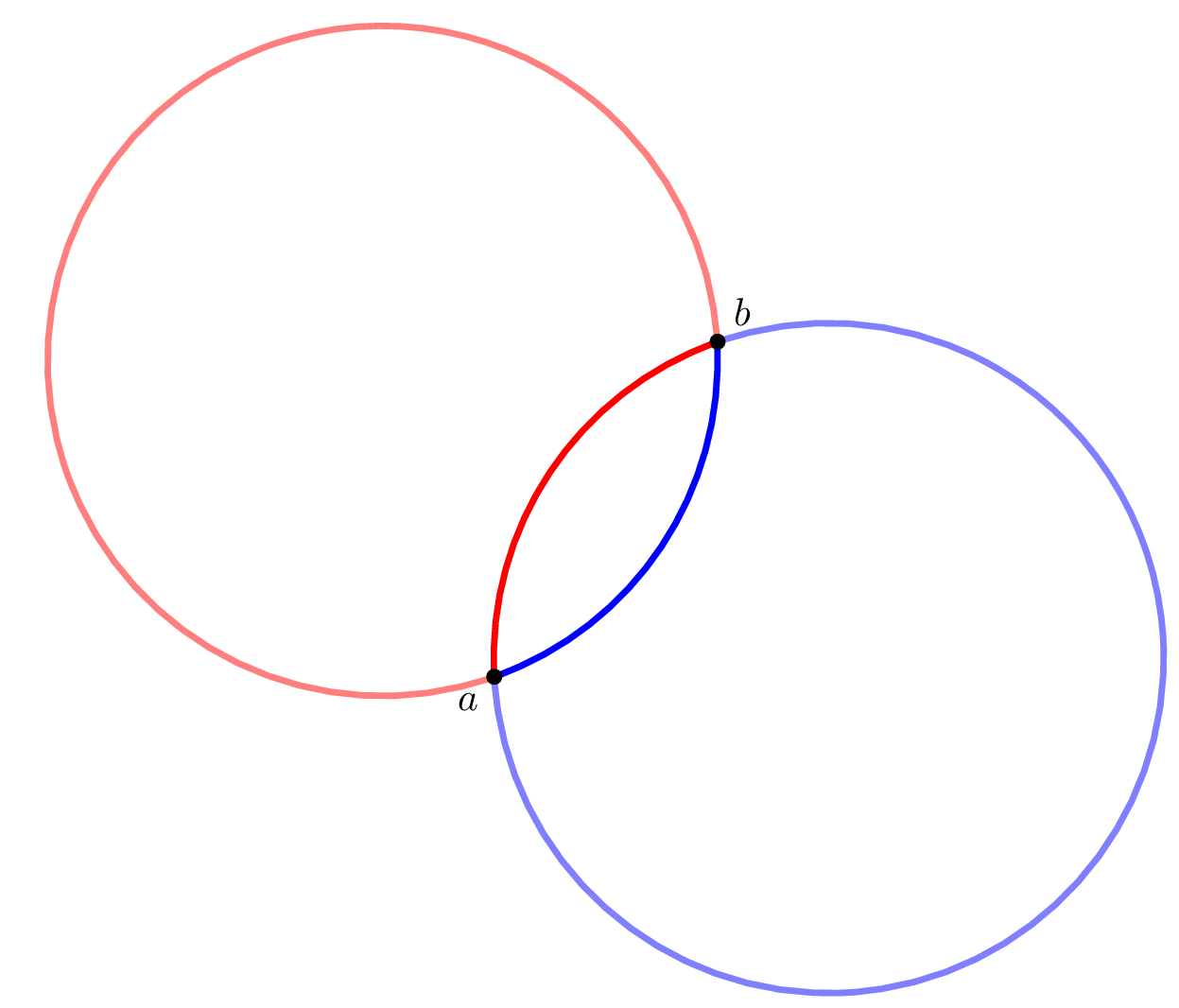
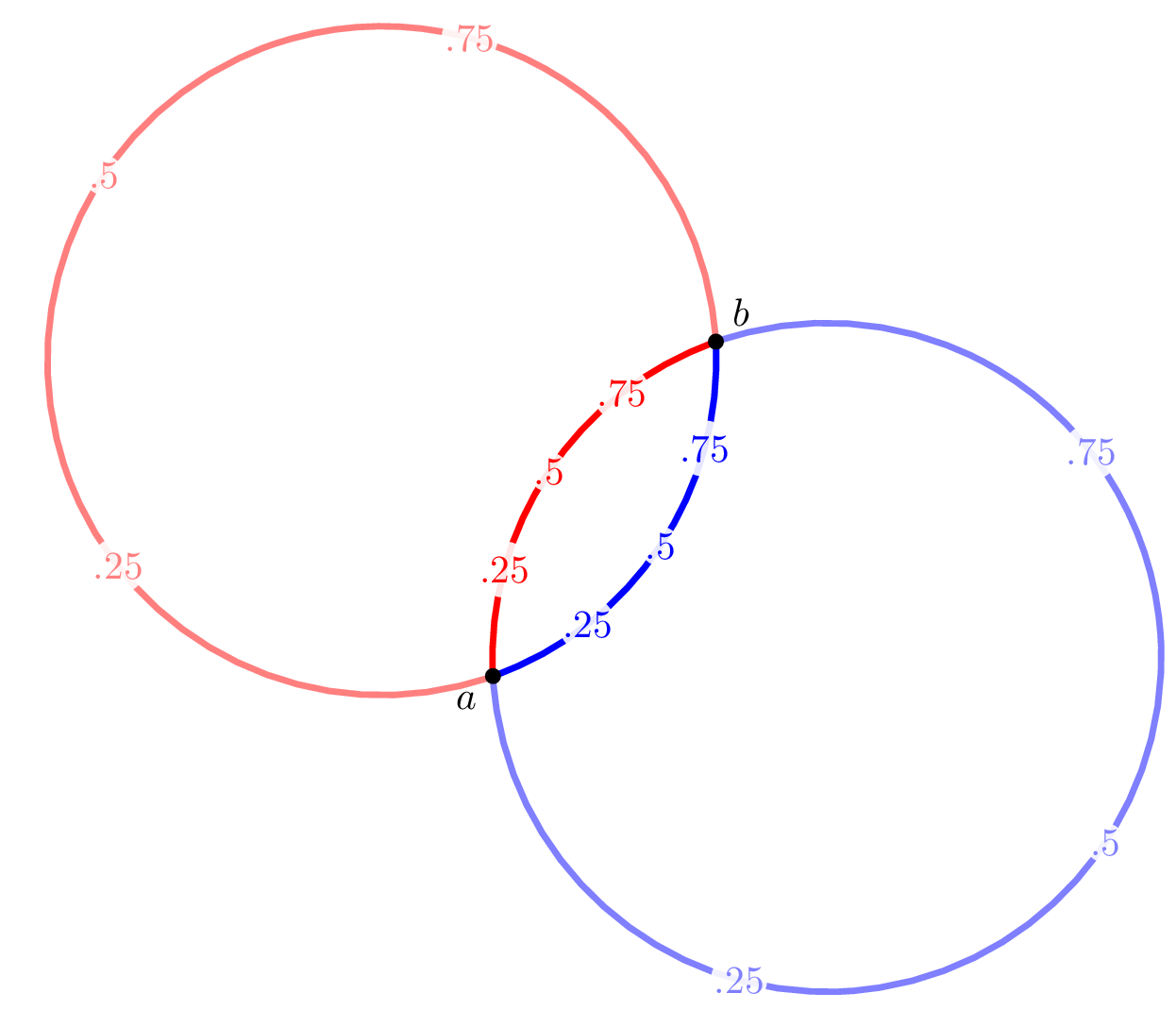
Um die Schnittpunkte zweier Kreise zu bestimmen, stellt
Für das Zeichen des Bogens um M von P nach Q zu schlagen, kommt nun noch ein letzter Befehl zum Einsatz: Das alles zusammengesetzt führt dann zu folgendem Beispiel:
Die folgende alte „Lösung“ berechnet den Radius falsch! Auch die Alternative, die im Kommentar vorgeschlagen wird, stimmt nicht! Bitte nicht verwenden. Ursprüngliche Antwort:Mit ein bisschen Geometrie, Mathematik und der Hilfe der
Edit Erst nach Beantwortung der Frage, wurde mir klar, dass es nicht um Kreise, sondern um Kreisbögen geht. Damit meine Arbeit nicht umsonst war, folgt daher eine Modifikation, die die ungewünschten Teile der Kreise durch Clipping entfernt:
Meine Berechnung stimmt nicht... vielleicht krieg ich das morgen gefixt, sonst lösch ich die Antwort wieder
(27 Aug '13, 23:26)
cgnieder
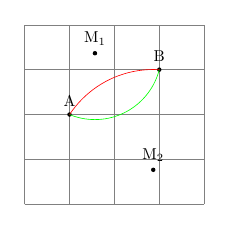
@Clemens Danke für die Info! Keine Eile, ich bin geduldig interessiert am Lernen und Verstehen. Insbesondere auch an Berechnung mit TikZ. Die zugrundeliegende Mathematik ist Beiwerk :-) hier sollte sich der Mittelpunkt z.B. als Schnitt vom Mittelsenkrechte zwischen den Punkten mit Kreis(en) durch einen der Punkte finden lassen, so ist es mir klar, nur nicht TikZ-Weise.
(27 Aug '13, 23:35)
Felix
@Felix statt Berichtigung (die m.E. den Weg so umständlich gemacht hätte, dass es den Aufwand nicht lohnt) hab ich eine Alternative gebracht...
(28 Aug '13, 16:01)
cgnieder
@Clemens Ich fürchte ich verstehe nicht, warum du
(28 Aug '13, 17:27)
Epllus
@Epllus Der Grund ist ein Denkfehler meinerseits. Es ist auch falsch!
(28 Aug '13, 17:32)
cgnieder
@Clemens: Vielleicht ist es besser, die Antworten mit dem nicht richtig berechneten Radius doch zu löschen, da andere den Code sonst eventuell doch nutzen: siehe hier auf mrunix
(31 Aug '13, 18:26)
esdd
Ergebnis 5 von 7
show 2 more comments
|