|
Hallo, Ich möchte mit LATEX möglichst einfach eine Grafik erstellen, die die komplexe Ebene zeigen soll. Darin möchte ich den "Korridor" PS: Das ist meine erste Frage, wie kann ich Latexumgebung für den mathematischen Text aktivieren? |
|
Ein Vorschlag mit
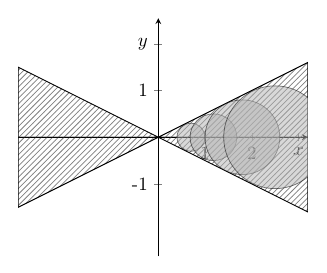
\documentclass[border=10pt]{standalone} \usepackage{pgfplots} \pgfplotsset{width=7cm, compat=1.8} \usetikzlibrary{patterns} \begin{document} \begin{tikzpicture} \begin{axis}[ axis lines = middle, xtick = {1, 2, 3}, xticklabels = {1, 2, $x$}, ytick = {-1, 1, 2}, yticklabels = {-1, 1, $y$}, samples = 160, domain = -3:3.2, xmin = -3, xmax = 3.2, ymin = -2, ymax = 2, axis equal, ] \foreach \funktion in {0.5*x, -0.5*x} { \addplot[line width=0.5pt, no markers, pattern = north east lines,pattern color=black!50] {\funktion} \closedcycle; } \foreach \x/\r in {0.7/0.3, 1.18/0.5, 1.8/0.8, 2.5/1.1} { \edef\kreis{\noexpand% \draw[fill=black!30, opacity=0.5] (axis cs:{\x},0) circle[radius=\r];} \kreis } \end{axis} \end{tikzpicture} \end{document}
@cQQkie Gerne! Poste ruhig weitere Fragen, aus denen heraus man tolle mathematische Illustrationen erstellen kann, macht ja Spaß! Ich habe nun sogar die Kategorie Funktionentheorie angelegt (wg. komplexer Zahlen) - ich denke "Tags" für Fachgebiete sind auch praktisch.
(26 Mär '14, 16:22)
stefan ♦♦
|
|
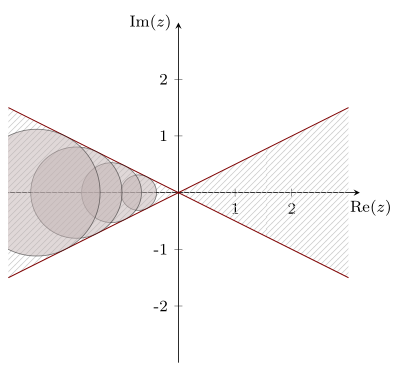
Der einfachste Weg wäre die auch von @Stefan erwähnte Nutzung der Bibliothek Man kann jedoch die Zeichnung auch nur mit TikZ erstellen und dabei ebenfalls tatsächlich die Fläche zwischen den Linien füllen. Die Radien \documentclass[margin=5pt,tikz]{standalone} \usetikzlibrary{patterns} \begin{document} \begin{tikzpicture}[ font=\footnotesize, % kleinere Schrift samples=2 % zum Plotten von Geraden reichen 2 Punkte ] % Koordinatensystem \draw[-stealth](-3,0)--(3.2,0)node[below right,xshift=-3mm]{Re$(z)$}; \draw[-stealth](0,-3)--(0,3)node[left]{Im$(z)$}; \clip(-3,-3)rectangle(3.2,3); \foreach \i in {1,2}\draw[very thin] (\i,2pt)--(\i,-2pt)node[below]{\i} (2pt,\i)--(-2pt,\i)node[left]{\i} (2pt,-\i)--(-2pt,-\i)node[left]{-\i}; % Füllung \fill[pattern =north east lines,pattern color=black!20] plot[domain=-3:3](\x,{0.5*\x})-- plot[domain=3:-3](\x,{-0.5*\x})--cycle; % Linien \draw[line width=.5pt,red!50!black] plot[domain=-3:3](\x,{0.5*\x}) plot[domain=3:-3](\x,{-0.5*\x}); % Kreise \foreach[evaluate=\x as \r using \x/sqrt(5)] \x in {0.7, 1.18, 1.8, 2.5} { \edef\kreis{\noexpand% \draw[fill=red!20!black!30, opacity=0.5] (-\x,0) circle[radius=\r];} \kreis } \end{tikzpicture} \end{document}
|

Herzlich willkommen auf der TeXwelt! Code im Text kann man mit Backticks (schrägen Hochkommata ...) markieren, oder bei mehreren Zeilen absetzen per Einrückung (4 Leerzeichen), dann erfolgt automatisch Syntax-Hervorhebung und Verknüpfung zum writeLaTeX Online-Compiler.