|
Nach dem Start von PGFplots.net experimentierte ich ein bisschen mehr mit pgfplots. Dabei fragte ich mich, wie ich das bei jeder Grafiksoftware tue, wie sich damit Fraktale darstellen lassen und ob es dabei evtl. nützliche oder interessante Aspekte gibt. Geschwindigkeit und Speicherplatz sind hier nebensächlich, Kapazitäten ändern sich eh mit der Zeit. Mich interessiert beispielsweise
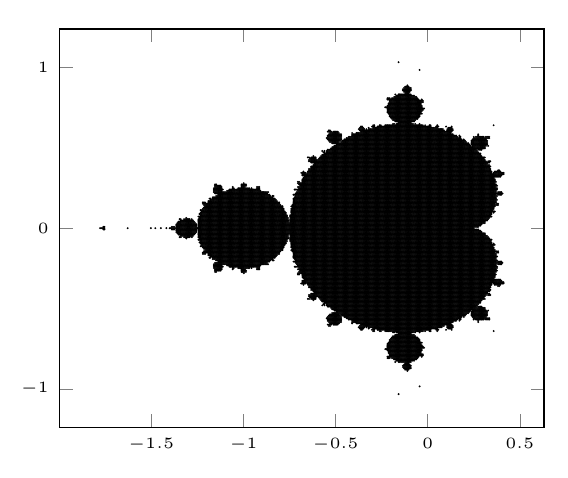
Es sind viele Fragen - wenn es sich ergibt, teilen wir das gern auf (kommentiert gern hierzu), jede interessante Antwort mit Beispiel ist willkommen. Hier habe ich ein Beispiel gemacht, inspiriert von Herberts Darstellung einer Weierstraß-Funktion. Die mit Lua errechneten Werte werden in einer Tabelle gespeichert (hier 0,6 MB groß), die dann mit geringem Aufwand geplottet wird. Kann pgfplots hier mehr übernehmen, während der Berechnung, so dass ich keine externen Tabelle brauche? Kann man Farbigkeit einbringen, wie in den bekannten bunten Mandelbrot-Bildern? \documentclass[border=10pt]{standalone} \usepackage{pgfplots} \pgfplotsset{width=7cm,compat=1.8} \usepackage{luacode} \begin{luacode} function mandelbrot(x0, x1, y0, y1, steps, max_iter, max) local dx = (x1-x0)/steps local dy = (y1-y0)/steps local cx = x0 local out=assert(io.open("tmp.data","w")) local x,y,cy,xtemp,ytemp,squaresum,iter while (cx <= x1) do cy = y0 while (cy <= y1) do squaresum = 0 x = 0 y = 0 iter = 0 while (squaresum <= max) and (iter < max_iter) do xtemp = x * x - y * y + cx ytemp = 2 * x * y + cy x = xtemp y = ytemp iter = iter + 1 squaresum = x * x + y * y end if (iter >= max_iter) then out:write(cx, " ", cy, " ", "\string\n") end cy = cy + dy end cx = cx + dx end out:close() end \end{luacode} \begin{document} \begin{tikzpicture} \directlua{mandelbrot(-2,1,-2,2,500,1000,4)} \begin{axis}[domain=-2:2,tick label style={font=\tiny},] \addplot [only marks, mark=*, mark size=0.06pt] table {tmp.data}; \end{axis} \end{tikzpicture} \end{document}
|
|
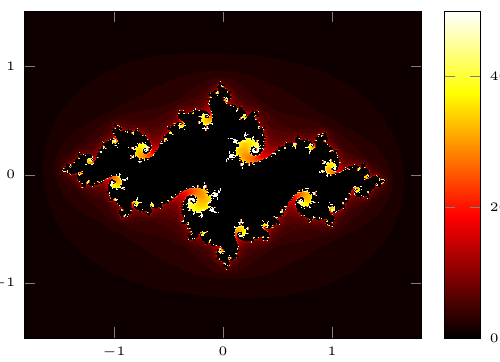
Eine Variante von Christians Antwort, um eine Julia-Menge zu plotten:
\documentclass[border=5pt]{standalone} \usepackage{pgfplots} \pgfplotsset{width=7cm,compat=1.8} \usepackage{luacode} \begin{luacode} function julia(cx,cy, max_iter, max) local x,y,xtemp,ytemp,squaresum,iter squaresum = 0 x = cx y = cy iter = 0 while (squaresum <= max) and (iter < max_iter) do xtemp = x * x - y * y - 0.742 ytemp = 2 * x * y + 0.1 x = xtemp y = ytemp iter = iter + 1 squaresum = x * x + y * y end local result = 0 if (iter < max_iter) then result = iter end -- result = squaresum -- io.write("" .. cx .. ", " .. cy .. " = " .. result .. " (iter " .. iter .. " squaresum " .. squaresum .. ") \string\n") tex.print(result); end \end{luacode} \begin{document} \begin{tikzpicture} \begin{axis}[ colormap/hot2, colorbar, axis equal, point meta max=50, tick label style={font=\tiny}, view={0}{90}] \addplot3 [surf, domain = -1.82:1.82, shader = interp, domain y = -1.5:1.5, samples = 350] {\directlua{julia(\pgfmathfloatvalueof\x,\pgfmathfloatvalueof\y,10000,4)} }; \end{axis} \end{tikzpicture} \end{document} |
|
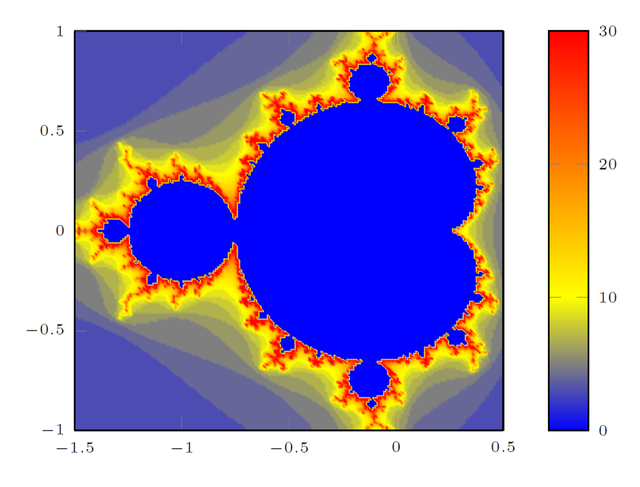
Im Grunde willst Du ja (x,y,f(x,y)) ausrechnen. In Deinem Fall hast Du lediglich "bestimmte" x y als tabelle exportiert (und dazu x und y in einem jeweils vordefinierten Interval gesamplt) und diese als scatter plot geladen. Einfacher ist es, wenn Du Hinzu kommt, dass Du vermutlich Farbverlaeufe sehen willst. Das geht am besten mit
\documentclass[border=10pt]{standalone} \usepackage{pgfplots} \pgfplotsset{width=7cm,compat=1.8} \usepackage{luacode} \begin{luacode} function mandelbrot(cx,cy, max_iter, max) local x,y,xtemp,ytemp,squaresum,iter squaresum = 0 x = 0 y = 0 iter = 0 while (squaresum <= max) and (iter < max_iter) do xtemp = x * x - y * y + cx ytemp = 2 * x * y + cy x = xtemp y = ytemp iter = iter + 1 squaresum = x * x + y * y end local result = 0 if (iter < max_iter) then result = iter end -- result = squaresum -- io.write("" .. cx .. ", " .. cy .. " = " .. result .. " (iter " .. iter .. " squaresum " .. squaresum .. ") \string\n") tex.print(result); end \end{luacode} \begin{document} \begin{tikzpicture} \begin{axis}[ colorbar, point meta max=30, tick label style={font=\tiny}, view={0}{90}] \addplot3 [surf,domain=-1.5:0.5,shader=interp,domain y=-1:1,samples=200] { \directlua{mandelbrot(\pgfmathfloatvalueof\x,\pgfmathfloatvalueof\y,10000,4)} }; \end{axis} \end{tikzpicture} \end{document} Dieses Listing braucht das expandierbare Macro Sehr schön!
(29 Mär '14, 00:23)
stefan ♦♦
|