|
Ich habe einen Polar-Plot in zwei Dimensionen: \documentclass{standalone} \usepackage{pgfplots} \usepgfplotslibrary{polar} \begin{document} \begin{tikzpicture} \begin{polaraxis}[ domain = -3600:3600, samples = 4000 ] \addplot[blue!50!black] {1 - sin(50*x/49) - sin(8*x)}; \end{polaraxis} \end{tikzpicture} \end{document}
Man sieht nicht die Umdrehungen um den Nullpunkt in nur zwei Dimensionen, denn der Plot ist nur modulo 360 Grad. Daher möchte ich die Grafik gern dreidimensional darstellen, so dass ich in der Höhe die Entwicklung des Plots mit wachsendem Winkel sehe. Wie kann man das machen? |
|
Man kann x einen Umlauf nur achen lassen, also etwa von -180 bis 180, und lässt einen weiteren Parameter y schrittweise wandern. Man addiert dann y*360 zum Winkelargument, beispielsweise mit y=0, 1, 2, ... und lässt dadurch den resultierenden Winkel das entsprechende größere Intervall durchlaufen.
Hier eine Umsetzung, mit der man nun sehen kann, wie die Kurve sich mit wachsendem Winkel entwickelt: \documentclass[border=10pt]{standalone} \usepackage{pgfplots} \begin{document} \begin{tikzpicture} \begin{axis}[ domain = -180:180, y domain = -19:19, samples y = 39, samples = 100, z buffer = sort, colormap/cool, grid ] \addplot3[data cs = polar, surf] ( {x}, {1 - sin(50*(x+360*y)/49) - sin(8*(x+360*y))}, {y} ); \end{axis} \end{tikzpicture} \end{document}
|

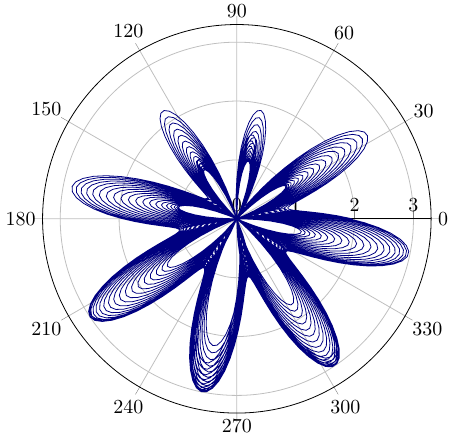
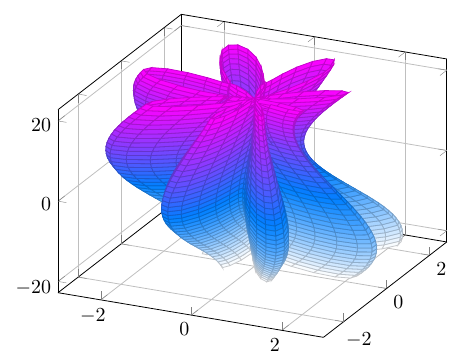
Die Frage ist zum Archivieren gedacht, kein Support benötigt. Antworten sind jedoch sehr willkommen! Ich werde selbst einen Lösungs-Vorschlag als Antwort schreiben.