|
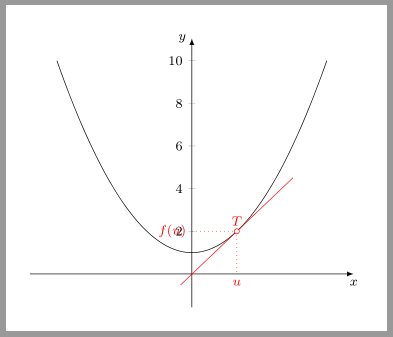
Warum ruiniert es mir den Graph, sobald ich an die Funktion \newcommand*\funktion[1]{(#1)^2 +1} So geht es: \newcommand*\funktion[1]{(#1)^2} \documentclass[margin=5mm]{standalone} \usepackage[ngerman]{babel} \usepackage{pgfplots} \pgfplotsset{compat=1.9} \begin{document} \begin{tikzpicture}[font=\footnotesize] % Dargestellte Funktion \newcommand*\funktion[1]{(#1)^2 +1} %* sin(deg(#1))^3 % Näherungsweise Ableitung / Tangentensteigung der Funktion \newcommand*\ableitung[1]{(\funktion{#1+0.01}-\funktion{#1})/0.01} % Tangente an die Funktion \newcommand*\tangente[2]{\ableitung{#2}*(#1-#2)+\funktion{#2}} \begin{axis}[axis lines=middle, enlargelimits, xlabel=$x$,xlabel style={anchor=north},xtick=\empty, ylabel=$y$,ylabel style={anchor=east},%ytick=\empty, x axis line style = {-latex}, y axis line style = {-latex}, ] \addplot[domain=-3:3,samples=200]{\funktion{\x}}; % Tangente zeichnen in T(u, f(u)) \pgfmathsetmacro{\u}{1} % Berührstelle u eingeben \pgfmathsetmacro{\Laenge}{1.25} % Länge der Tangente eingeben % Tangente \addplot[domain=\u-\Laenge:\u+\Laenge, red]{\tangente{\x}{\u}}; % Koordinaten des Berührpunktes und seiner Fusspunkte \coordinate (P) at (axis cs: \u,{\funktion{\u}}) ; \coordinate (Q) at (axis cs:0,{\funktion{\u}}) ; \coordinate (R) at (axis cs:\u,0) ; \draw[red,dotted] (P) -- (Q) node[left] {$f(u)$} ; \draw[red,dotted] (P) -- (R) node[below] {$u$} ; % Berührpunkt T(u, f(u)) \draw[red, fill=white] (axis cs: \u, {\funktion{\u}}) circle[radius=1.5pt] node[above, red] {$T$}; \end{axis} \end{tikzpicture} \end{document} |
|
Der Befehl \newcommand*\ableitung[1]{(\funktion{#1+0.01}-\funktion{#1})/0.01} bei Verwendung des von Dir definierten \newcommand*\ableitung[1]{((#1+0.01)^2 +1-(#1)^2 +1)/0.01} Beachte das Du müsstest also die Summe in Deiner Definition von \newcommand*\funktion[1]{((#1)^2 +1)}
Alternativ kannst Du auch die Bibliothek \documentclass[margin=5mm]{standalone} \usepackage[ngerman]{babel} \usepackage{pgfplots} \pgfplotsset{compat=1.9} \usetikzlibrary{math} \begin{document} \begin{tikzpicture}[font=\footnotesize] \tikzmath{ function funktion(\x) {return \x^2+1;}; function ableitung(\x) {return (funktion(\x+0.01)-funktion(\x))/0.01;}; function tangente(\x, \u) {return ableitung(\u)*(\x-\u)+funktion(\u);}; } \begin{axis}[ axis lines=middle, enlargelimits, xlabel=$x$,xlabel style={anchor=north},xtick=\empty, ylabel=$y$,ylabel style={anchor=east},%ytick=\empty, x axis line style = {-latex}, y axis line style = {-latex}, ] \addplot[domain=-3:3,samples=200]{funktion(x)}; % Tangente zeichnen in T(u, f(u)) \pgfmathsetmacro{\u}{1} % Berührstelle u eingeben \pgfmathsetmacro{\Laenge}{1.25} % Länge der Tangente eingeben % Tangente \addplot[domain=\u-\Laenge:\u+\Laenge, red]{tangente(x,\u)}; % Koordinaten des Berührpunktes und seiner Fusspunkte \coordinate (P) at (axis cs: \u,{funktion(\u)}) ; \coordinate (Q) at (axis cs:0,{funktion(\u)}) ; \coordinate (R) at (axis cs:\u,0) ; \draw[red,dotted] (P) -- (Q) node[left] {$f(u)$} ; \draw[red,dotted] (P) -- (R) node[below] {$u$} ; % Berührpunkt T(u, f(u)) \draw[red, fill=white] (axis cs: \u, {funktion(\u)}) circle[radius=1.5pt] node[above, red] {$T$}; \end{axis} \end{tikzpicture} \end{document} Wenn Du Ah sehr gut. Ich schreibe
(02 Apr '17, 23:32)
cis
|