|
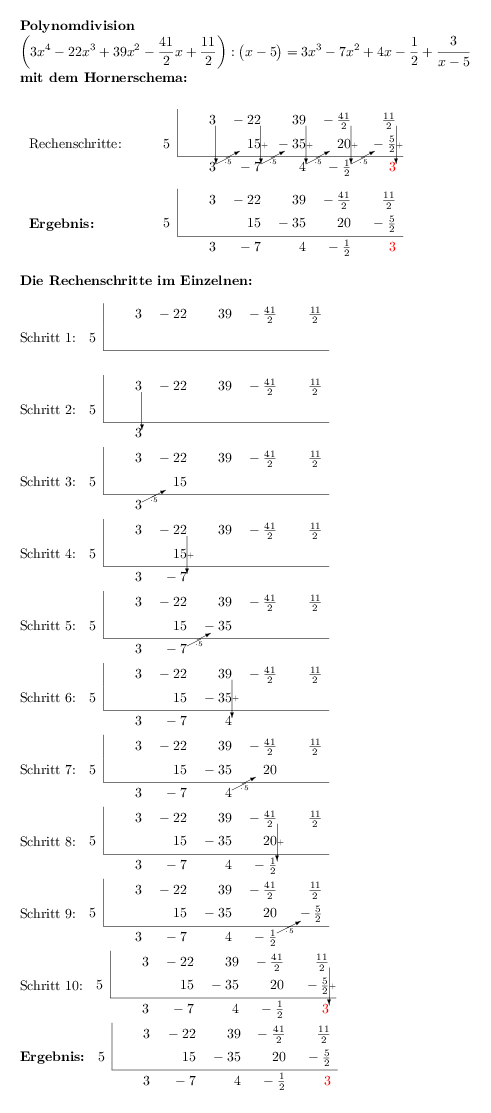
Frage zur Selbstbeantwortung. Die Frage ist zum Archivieren gedacht, kein Support benötigt. Ich beantworte die Frage auch selbst. Antworten sind jedoch sehr willkommen! Mitunter ist es praktisch, sich zu einer längeren Rechnung die Rechenschritte einzeln anzuschauen. Wie kann ich mir für eine Polynomdivision sämtliche Rechenschritte für das Hornerschema anzeigen lassen? |
|
Man kann bei Öffne in Overleaf
\documentclass[margin=5mm, varwidth]{standalone} \usepackage{polynom, xcolor, pgffor, amsmath} \usepackage{tikz} \usetikzlibrary{matrix} % Für alignment-Darstellung \begin{document} % Polynome abspeichern: \polyadd{\Zaehler}{3x^4 - 22x^3 + 39x^2 - \frac{41}{2}x + \frac{11}{2}}{0}% Trick \polyadd{\Nenner}{x-5}{0}% % Trick: 'Nenner + 0' somit gespeichert.... \polydiv\QuotientOhneRest\Zaehler\Nenner \polyset{tutor=true, resultstyle=\color{red}} {\bfseries Polynomdivision \\ $\displaystyle \left( \polyprint\Zaehler \right) : \left( \polyprint\Nenner \right) = \polyprint\QuotientOhneRest + \frac{\polyprint{\polyremainder}}{\polyprint\Nenner}$ \\ mit dem Hornerschema:} \\ \tikz[]{ \matrix[matrix of nodes, anchor=base west, text width=3cm,]{ Rechenschritte: & {\polyhornerscheme[x=5, stage=10, tutorlimit=9]\Zaehler }\\ \textbf{Ergebnis:} & {\polyhornerscheme[x=5]\Zaehler} \\ }} {\bfseries Die Rechenschritte im Einzelnen:} \\ \foreach \Schritt in {1,...,11}{% \ifnum\Schritt<11% Schritt \Schritt: \polyhornerscheme[x=5, stage=\Schritt]\Zaehler \\% \else% \textbf{Ergebnis:} \polyhornerscheme[x=5, stage=\Schritt]\Zaehler% \fi} \end{document} |