|
Hallo zusammen, folgender Code sollte Entropy der Binomialverteilung für n=1,..,5 plotten, tut es aber nicht. Wo ist das Problem? Öffne in Overleaf
\documentclass{article} \usepackage{pgfplots} \begin{document} \begin{tikzpicture}[scale=1] % Axis \node (1) at (0,6.5) {$H(x)$}; \node (2) at (7.5,0) {$p$}; \begin{axis}[ samples=100, smooth, domain=0.01:0.99, ] \foreach \N in {1,...,5} {% \addplot+ [mark = none] gnuplot[raw gnuplot] {% set samples 100; b(k, n, p) = n!/(k!*(n-k)!)*p**k*(1-p)**(n-k); plot[0.01:0.99] sum [k=0:\N] -b(k,\N,x)*log2(b(k,\N,x)) }; \addlegendentryexpanded{$B_\N$} } \end{axis} \end{tikzpicture} \end{document}
Dieser Frage ist "Community Wiki" markiert.
|
|
Ich lese einfach mal die Fehlermeldung für dich
Wie man sieht gibt es die Funktion Öffne in Overleaf
\documentclass{article} \usepackage{pgfplots} \begin{document} \begin{tikzpicture}[scale=1] % Axis \node (1) at (0,6.5) {$H(x)$}; \node (2) at (7.5,0) {$p$}; \begin{axis}[ samples=100, smooth, domain=0.01:0.99, ] \foreach \N in {1,...,5} {% \addplot+ [mark = none] gnuplot[raw gnuplot] {% set samples 100; b(k, n, p) = n!/(k!*(n-k)!)*p**k*(1-p)**(n-k); plot[0.01:0.99] sum [k=0:\N] -b(k,\N,x)*log(b(k,\N,x))/log(2) }; \addlegendentryexpanded{$B_\N$} } \end{axis} \end{tikzpicture} \end{document} |

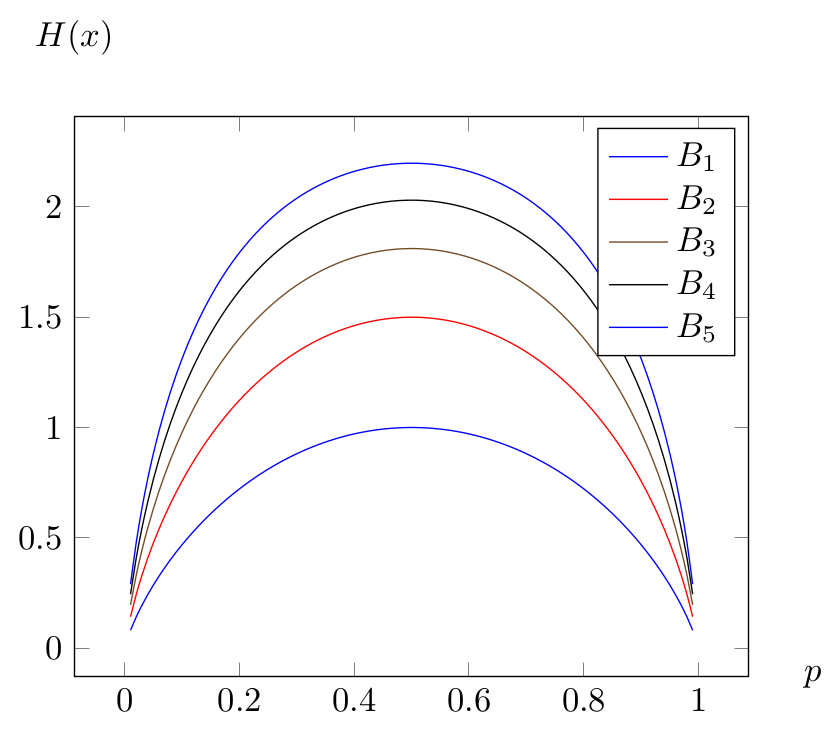
Willkommen auf TeXwelt.de! Ich habe einmal den Code vervollständigt. Hier sollte man besser komplette, übersetzbare (kurze) Codes posten, damit man überhaupt testen kann. Sonst verbleibt als Antwortmöglichkeit sowas wie "pgfplots nicht geladen" oder "keine geeignete Dokumentklasse" weil die Präambel fehlt. Zum Problem: man muss mit Option
shell-escapeübersetzen, damit Gnuplot läuft. Hast Du das?