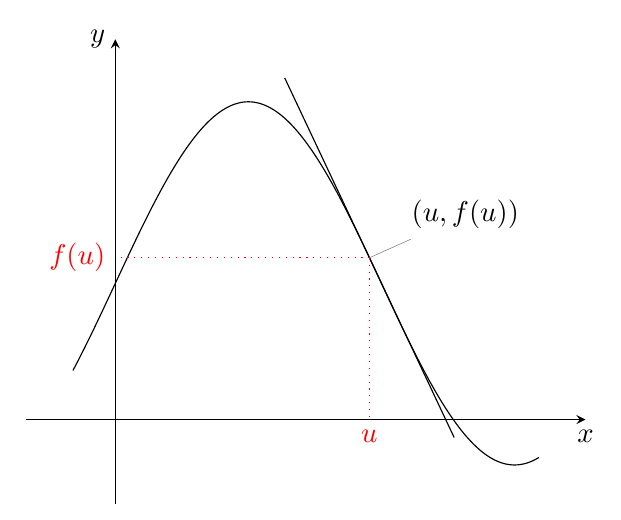
|
Mit
|
|
Eine Tangente an (u|f(u)) ist ja gegeben durch
Mit Deinen beiden Makros bist Du also schon fast am Ziel für den Automatismus:
Wenn man die Ableitung nicht kennt, gibt es scheints keine einfache Lösung mehr, richtig?
(02 Apr '17, 13:57)
cis
@cis das Tangentenproblem ist in der Schule in der Regel das, mit dem die Ableitung im Matheunterricht eingeführt wird, da man merkt, dass man ohne sie die Tangentensteigung nicht bzw nur näherungsweise bestimmen kann…
(02 Apr '17, 14:01)
cgnieder
Ne, mich interessiert, ob eine reine pgf-Lösung für beliebige Kurven möglich ist; über die Ableitungsfunktion ist es klar.
(02 Apr '17, 15:41)
cis
Die reinen Tikz-Lösungen, die ich geshen habe, sehen kompliziert aus. Ich empfehle, die Ableitung in der Form
(03 Apr '17, 10:28)
cis
|
|
Hier ist noch ein anderer Ansatz, bei dem zunächst ein Befehl für das Zeichnen einer Geraden durch einen Punkt definiert wird, der sich auch für das Zeichnen einer Tangente bei gegebener Funktion und Ableitung eignet. Außerdem wird für das Beschriften den Punkte ebenfalls ein eigener Befehl definiert. |