|
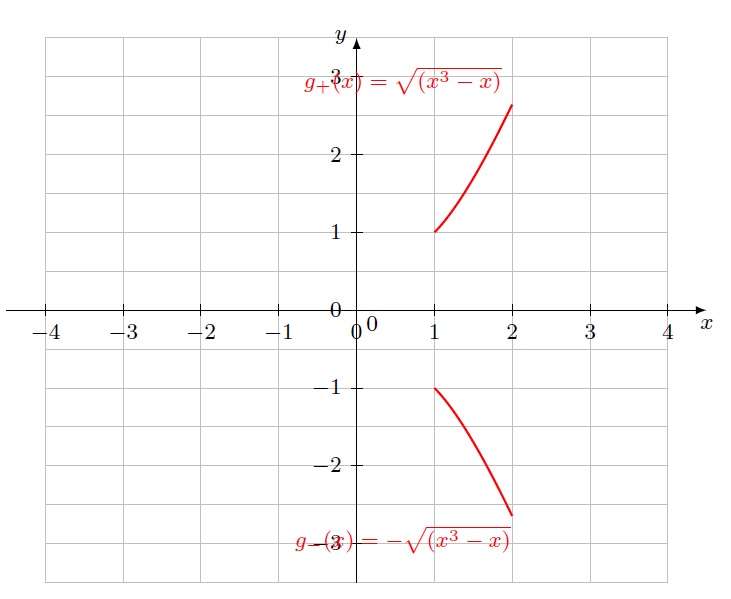
Ich habe es jetzt so versucht mit den zwei Wurzelfunktionen, leider klappt es nicht so ganz. Ich wollte y^2=x^3-x zeichnen. Habe es so wie oben gemacht und erhielt das Bild
Es sollte jedoch so ungefähr aussehen:
|
|
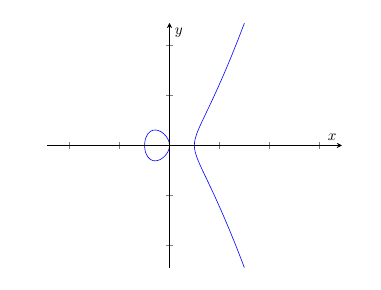
Mit pgfplots und mit Hilfe von gnuplot kann man sogenannte Konturplots zeichnen.
\documentclass{article} \usepackage{pgfplots} \begin{document} \begin{tikzpicture} \begin{axis}[ view = {0}{90}, axis x line = middle, axis y line = middle, axis equal, xlabel = {$x$}, ylabel = {$y$}, restrict x to domain = -2.2:3 ] \addplot3 [contour gnuplot = {labels = false}, samples=100] { y^2 - x^3 + x }; \end{axis} \end{tikzpicture} \end{document}
Hinweise:
|
|
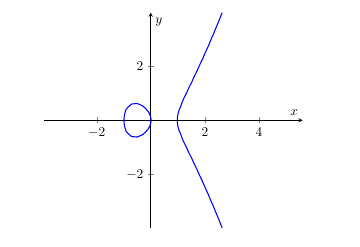
Eine alternative Lösung mit pgfplots und \documentclass{article} \usepackage{pgfplots} \begin{document} \begin{tikzpicture} \begin{axis}[ axis x line = middle, axis y line = middle, axis equal, xlabel = {$x$}, ylabel = {$y$}, restrict y to domain = -4:4, ] \addplot + [ no markers, raw gnuplot, thick, ] gnuplot { set contour base; set cntrparam levels discrete 0.01; unset surface; set view map; set isosamples 300; splot y**2 - x**3 + x; }; \end{axis} \end{tikzpicture} \end{document}
|

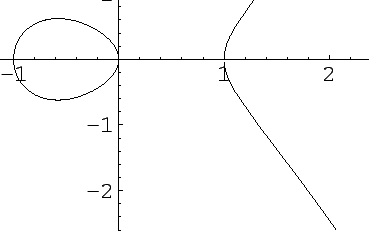
Ich habe dazu in meiner AW ein paar Sachen ergänzt
@karra Mir fällt noch ein: contour plot der dreidimensionalen Funktion
z=y^2-x^3+ax+b, also Schnitt mit derz=0-Ebene, evtl. schreib ich noch was dazu am Abend (bin unterwegs).Ja, generell mußt Du stückweise stetige Funktionen auch stückweise zeichnen. Das kann man mitunter auch automatisieren, z.B. mit Schleifen o.ä., aber das schauen wir uns dann an, wenn es soweit ist.
Wie sieht es denn aus wenn ich eine Funktion habe, bei der die "linke Seite" und die "rechte Seite" sich im Nullpunkt schneiden? Die Funktion ist ja dann nicht stückweise stetig, aber im ganzen betrachten kann ich sie auch nicht...
@karra Ich habe den Kommentar mit der Frage nach der "Schleifenfunktion" in eine separate Frage umgewandelt und eine Antwort gepostet: Wie kann man eine nicht eindeutige Funktion plotten?. Wir mischen hier nicht Antworten und Fragen, sondern ordnen nach einzelnen Fragen und ihren konkreten Anworten, so kann man besser sortieren und suchen auf lange Sicht.