|
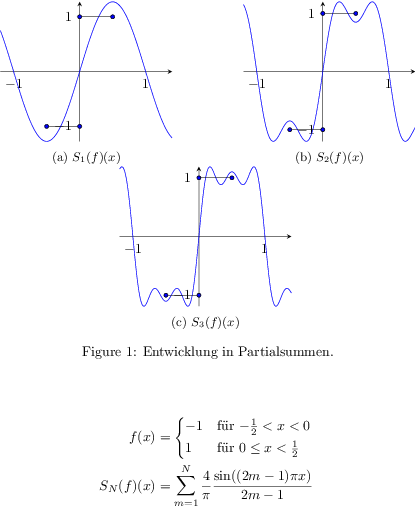
Hallo, ich würde gerne drei verschieden Plots auf einer Seite einrichten. Am besten alle drei nebeneinander. In jedem Plot soll die Funktion f gezeichnet sein und zudem eine Partialsumme SN [siehe Bild]. Man kann es für die Partialsumme sicherlich einrichten, dass man (bzw. später ich) noch den Paramter N variieren lassen kann. Vielleicht hat da ja jemand Ideen. Ich habe in meinem Dokument schon Plots mit TikZ, die so ähnlich aussehen wie der Quellcode unten (zur Orientierung des Stils). Hier sind f und SN und ein kleiner Plott mit Geogebra für N=1, N=2 und N=3. Ich hoffe, man kann sich vorstellen, was ich vorhabe :-) LG Niklas
\begin{tikzpicture} %Raster zeichnen %\draw [color=gray!50] [step=5mm] (0,-2) grid (7,2); % Achsen zeichnen \draw[->,thick] (-4,0) -- (4,0) node[right] {$x$}; \draw[->,thick] (0,-2.3) -- (0,2.3) node[above] {$y$}; % Achsen beschriften \draw (1,-.2) -- (1,0) node[below=4pt] {$\scriptstyle1$}; \draw (3.141,-.2) -- (3.141,0) node[below=4pt] {$\scriptstyle \pi$}; \foreach \y in {-2,-1,0,1,2} \draw (-.1,\y) -- (.1,\y) node[left=4pt] {$\scriptstyle\y$}; \end{tikzpicture} |
Nur
|
|
Hier mal eine Nur-Tikz Lösung. Sie kommt mit elementaren Mitteln aus und die Rechendauer hält sich, bei nicht zu großem N, in Grenzen:
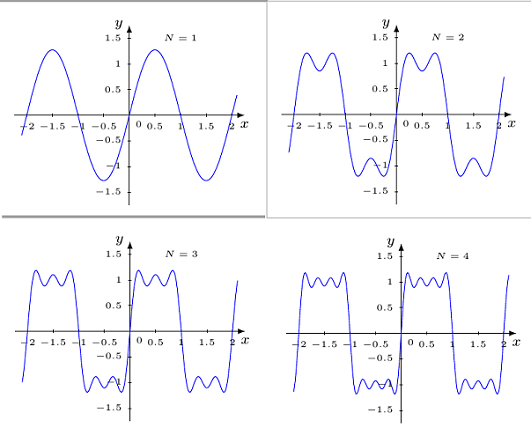
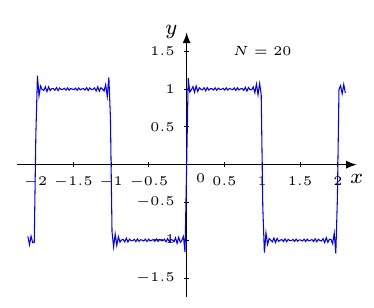
\documentclass[margin=2.5mm]{standalone} \usepackage{tikz} \usetikzlibrary{fpu} %Funktion definieren \def\N{3} % obere Summationsgrenze \def\x{\noexpand\x} % \x nicht ändern in \edef \edef\Gibbs{0} % Gibbs_0 = S_0 := 0 \edef\Mm{-1} % M_0 :=-1; M_(m+1) = M_m + 2 bzw. M_m = 2m-1 \foreach \m in {1,...,\N} {% %Summe von 1 bis N \global\edef\Mm{\Mm+2} % M_(m+1) = M_m + 2; \global\edef\Gibbs{ \Gibbs + (4*sin(((\Mm)*pi*\x) r)/(pi*(\Mm)) } }% %======== \begin{document} %======== \begin{tikzpicture}[>=latex, font=\tiny] %\node[] at (0,0) {\Mm}; % Zur Kontrolle %\node[] at (0,-1){\Gibbs}; % der Berechnung % \draw[help lines] (-2,-1.25) grid (2,1.0); %Achsen Zeichnen \draw[->] (-2.25,0) -- (2.25,0) node[below] {\footnotesize$x$}; \draw[->] (0,-1.75) -- (0,1.75) node[left] {\footnotesize$y$}; % Achsen beschriften \foreach \x in {-2,-1.5,...,-0.5,0.5,1,...,2} \draw (\x,-1pt) -- (\x,1pt) node[below=2pt] {$\x$}; \foreach \y in {-1.5,-1,-0.5, 0.5,1,1.5} \draw (-1pt,\y) -- (1pt,\y) node[left=2pt] {$\y$}; \node[below right]{$\scriptstyle0$}; %Funktion zeichnen \draw[color=blue, /pgf/fpu, /pgf/fpu/output format=fixed] plot[domain=-2.1:2.1, samples=201, smooth] (\x, {\Gibbs}); \node at (1.0,1.5) {$N=\N$}; \end{tikzpicture} %======== \end{document} %======== €dit: Wegen der Zusatzfrage, nach der "Platzierung", eine kleine Ergänzung: \documentclass[a4paper]{article} \usepackage{tikz} \usetikzlibrary{fpu} \newcommand{\PlotGibbs}[1]{%%%%%%%%%%% %Funktion definieren \def\N{#1} % obere Summationsgrenze \def\x{\noexpand\x} % \x nicht ändern in \edef \edef\Gibbs{0} % Gibbs_0 = S_0 := 0 \edef\Mm{-1} % M_0 :=-1; M_(m+1) = M_m + 2 bzw. M_m = 2m-1 \foreach \m in {1,...,\N} {% %Summe von 1 bis N \global\edef\Mm{\Mm+2} % M_(m+1) = M_m + 2; \global\edef\Gibbs{ \Gibbs + (4*sin(((\Mm)*pi*\x) r)/(pi*(\Mm)) } }% \begin{tikzpicture}[>=latex, font=\tiny] %\node[] at (0,0) {\Mm}; % Zur Kontrolle %\node[] at (0,-1){\Gibbs}; % der Berechnung % \draw[help lines] (-2,-1.25) grid (2,1.0); %Achsen Zeichnen \draw[->] (-2.25,0) -- (2.25,0) node[below] {\footnotesize$x$}; \draw[->] (0,-1.75) -- (0,1.75) node[left] {\footnotesize$y$}; % Achsen beschriften \foreach \x in {-2,-1.5,...,-0.5,0.5,1,...,2} \draw (\x,-1pt) -- (\x,1pt) node[below=2pt] {$\x$}; \foreach \y in {-1.5,-1,-0.5, 0.5,1,1.5} \draw (-1pt,\y) -- (1pt,\y) node[left=2pt] {$\y$}; \node[below right]{$\scriptstyle0$}; %Funktion zeichnen \draw[color=blue, /pgf/fpu, /pgf/fpu/output format=fixed] plot[domain=-2.1:2.1, samples=201, smooth] (\x, {\Gibbs}); \node at (1.0,1.5) {$N=\N$}; \end{tikzpicture} }%%%%%%%%%%%%%%%%%%%%%% %======== \begin{document} %======== Betrachten wir die F{\"a}lle N = 1, 4 und 7: \\ \begin{tabular}{clclc} \PlotGibbs{1} & \PlotGibbs{4} \\ \PlotGibbs{7} & \end{tabular} %oder ähnlich..... %======== \end{document} %======== €dit2: Ich habe noch eine Ergänzung mit der Bibliothek fpu vorgenommen, das erlaubt auch höhere Summationsgrenzen N (ohne fpu nur bis N=22). Damit ist die Lösung nicht mehr, wie angestrebt, 100% elementar; aber, wie gesagt, wenn man keine zu großen N-Werte braucht, kann man das auch weglassen. Eine ebenfalls sehr schöne Lösung!
(23 Apr '14, 17:45)
uniQue_
Wegen dem Platzierungsproblem kann man sich das Leben leicht machen - siehe edit...
(23 Apr '14, 18:36)
cis
|
|
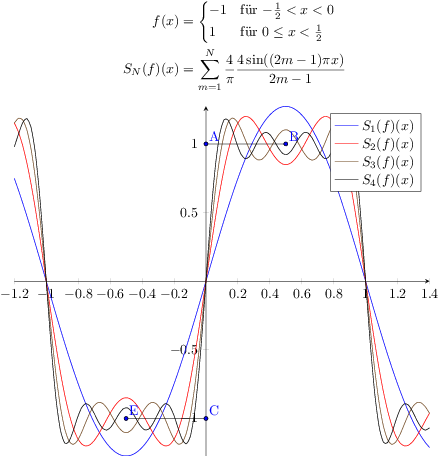
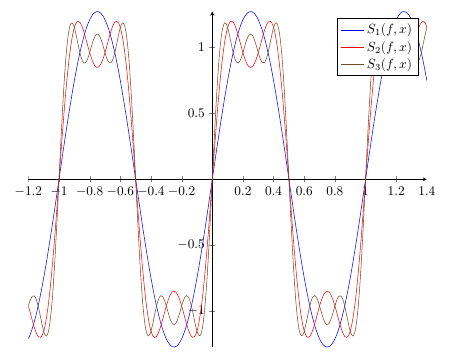
Eine Lösung mit gnuplot und pgfplots, es geht natürlich auch gnuplot mit nur TikZ, doch ich mag den Komfort von pgfplots. Achseneinstellungen habe ich von Henri übernommen, der Plot geschieht als \documentclass{standalone} \usepackage{pgfplots} \begin{document} \begin{tikzpicture} \begin{axis}[ no markers, samples=100, smooth, domain=-1.2:1.4, axis lines=middle, width=\linewidth ] \foreach \N in {1,2,3} {% \addplot+ [mark = none] gnuplot[raw gnuplot] {% set samples 200; s(m, x) = 4/((2*m-1)*pi)*sin(2*(2*m-1)*pi*x); plot[-1.2:1.4] sum [m=1:\N] s(m,x) }; \addlegendentryexpanded{$S_\N(f,x)$} } \end{axis} \end{tikzpicture} \end{document}
Oh, inzwischen hat Henri eine gnuplot-Lösung hinzugefügt. Sehr schön! Dann kann ich meine ganz ähnliche Antwort löschen. Zumindest zeigt das die Beteiligung hier. :-)
(22 Apr '14, 21:43)
stefan ♦♦
+1: Trotzdem ist ein Fehler drin. Es sollte
(22 Apr '14, 22:29)
Henri
|

@cis: Man kann mit directluat{} eine Funktion schreiben und diese für den Plot aufrufen. Ich bin überhaupt kein Eperte und hoffe deshalb, dass jemand eine schöne Lösung oder Idee hat.