|
Ich möchte einen Lorenz-Attraktor grafisch mit LaTeX darstellen. Hierfür erzeugte ich die Daten durch ein kleines Python-Programm, der Originalcode stammt von Chong Zan Kai und wurde von mir auf das nötigste reduziert sowie um die Ausgabe in eine Datei ergänzt. from scipy.integrate import odeint import scipy def lorenz_int(initial, t): x = initial[0] y = initial[1] z = initial[2] sigma = 10 rho = 28 beta = 8.0/3 x_dot = sigma * (y - x) y_dot = x * (rho -z) - y z_dot = x * y - beta* z return [x_dot, y_dot, z_dot] initial = [0, 1, 1.05] t = scipy.arange(0, 100, 0.01) lorenz_sol = odeint(lorenz_int, initial, t) pfile=open('lorenz2.dat','w') for i in lorenz_sol: pfile.write("%2.2f %2.2f %2.2f \n" % (i[0],i[1],i[2])) pfile.close() Die damit erzeugte Datei kann man hier herunterladen. Wie kann man die dreidimensionalen Daten gut darstellen? Mögliche Ansätze und Ideen:
Eine erste Version poste ich als Antwort im Anschluss an die Frage, unter Verwendung von |
|
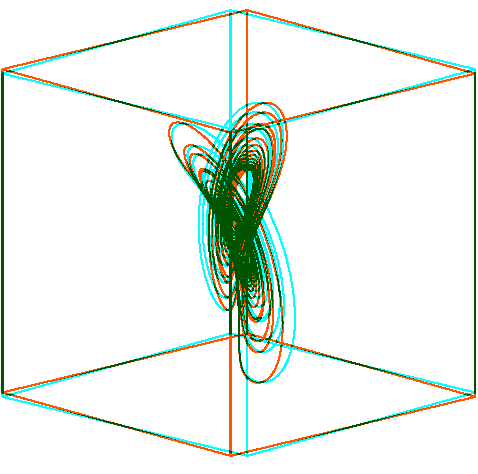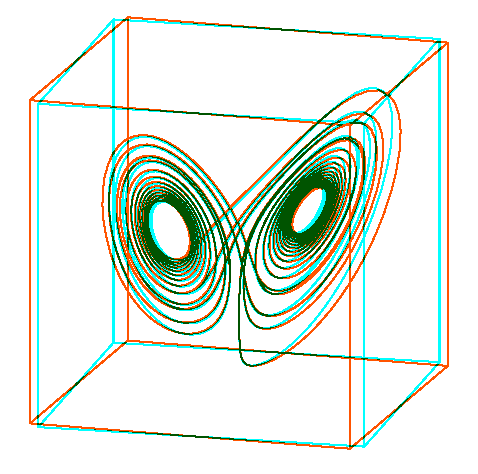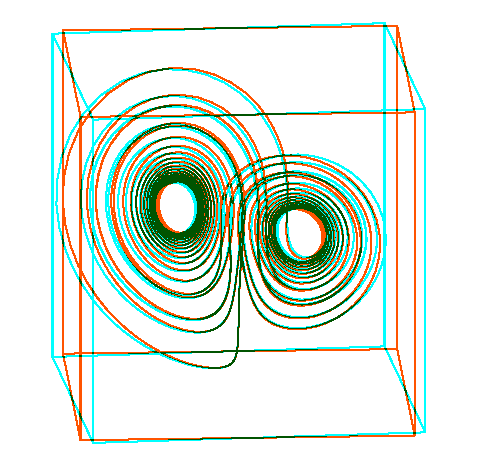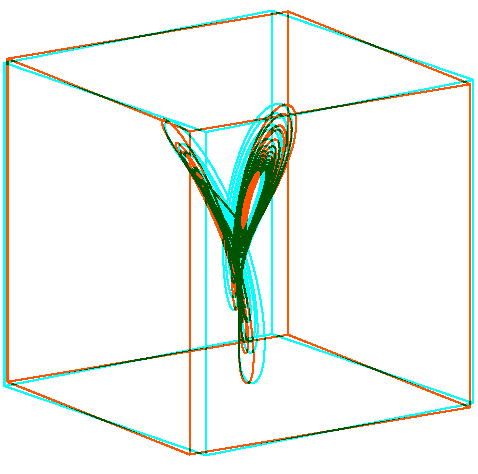
Für PSTricks gibt es das Paket Hier ein Attraktor als Anaglyph-3D erzeugt mit
Der LaTeX-Quelltext wird mit convert -density 100 alpha off <mydoc>.pdf <mydoc>.gif composite -stereo +0 <mydoc>.gif[0] <mydoc>.gif[36] Stereo.gif i=1 while [ $i -lt 36 ] do composite -stereo +0 <mydoc>.gif[$i] <mydoc>.gif[$((i+36))] tmp.gif convert -loop 0 Stereo.gif tmp.gif Stereo.gif ((i++)) done Quelltext: \documentclass{article} \usepackage[tightpage,active]{preview} \usepackage{pst-ode,pst-3dplot,multido} \newcommand\lorenzattraktor[2]{% #1: Farbe, #2: Winkel \ifdefined\lorenz\else% \pstVerb{% /alpha 10 def /beta 28 def /gamma 8 3 div def }% \pstODEsolve[algebraic]{lorenzXYZ}{0 1 2}{0}{25}{2501}{10 10 30}{ alpha*(x[1]-x[0]) | x[0]*(beta-x[2]) - x[1] | x[0]*x[1] - gamma*x[2] }% \gdef\lorenz{}% \fi% \begin{pspicture}(-6.05,-2)(6.05,10) \psset{unit=0.17cm,linecolor=#1,Alpha=#2,Beta=15} \listplotThreeD{lorenzXYZ} \psset{unit=0.425cm} \pstThreeDNode(0,0,0){O} \pstThreeDNode(0,0,5){Z} \pstThreeDNode(5,0,0){X} \pstThreeDNode(0,5,0){Y} \pstThreeDNode(-10,-10,0){A} \pstThreeDNode(-10,-10,20){B} \pstThreeDNode(-10,10,20){C} \pstThreeDNode(-10,10,0){D} \pstThreeDNode(10,-10,0){E} \pstThreeDNode(10,-10,20){F} \pstThreeDNode(10,10,20){G} \pstThreeDNode(10,10,0){H} \pspolygon(A)(B)(C)(D) \pspolygon(E)(F)(G)(H) \psline(A)(E) \psline(B)(F) \psline(D)(H) \psline(C)(G) \end{pspicture}% } \begin{document}% \multido{\iRed=43+10}{36}{% \begin{preview}% \definecolor{orng}{rgb}{1,0.33,0}% \lorenzattraktor{orng}{\iRed}% \end{preview}% }% \multido{\iCyan=47+10}{36}{% \begin{preview}% \definecolor{cyn}{rgb}{0,1,1}% \lorenzattraktor{cyn}{\iCyan}% \end{preview}% }% \end{document}
Hier ein Beispiel, das
\documentclass[border=10pt]{standalone} \usepackage{filecontents} \usepackage{pgfplots} \pgfplotsset{compat=1.8} \begin{filecontents}{xyz.tex} \input pst-ode \pstVerb{ /alpha 10 def /beta 28 def /gamma 8 3 div def }% \pstODEsolve[ algebraic, saveData % schreibt Ergebnis in lorenzXYZ.data % erfordert ps2pdf -dNOSAFER ]{lorenzXYZ}{0 1 2}{0}{100}{10001}{0 1 1.05}{ alpha*(x[1]-x[0]) | x[0]*(beta-x[2]) - x[1] | x[0]*x[1] - gamma*x[2] } \bye \end{filecontents} \immediate\write18{tex xyz} \immediate\write18{dvips xyz} \immediate\write18{ps2pdf -dNOSAFER xyz.ps} \begin{document} \begin{tikzpicture} \begin{axis}[ xmin = -25, xmax = 25, ymin = -25, ymax = 25, zmin = 0, zmax = 50, hide axis, ] \addplot3[mark=none, mesh, shader=interp, color=black, opacity=0.2] file {lorenzXYZ.dat}; \end{axis} \end{tikzpicture} \end{document}
@AlexG Danke! Mir ging es vorwiegend um die Darstellung, doch
(27 Jun '14, 16:46)
stefan ♦♦
@AlexG Danke, diese Kombination
(27 Jun '14, 17:24)
stefan ♦♦
Habe die Kurve neu berechnet mit denselben Anfangswerten, Länge des Integrationsintervalls und Ausgabeschrittweite wie in Stefans
(27 Jun '14, 17:40)
AlexG
|
|
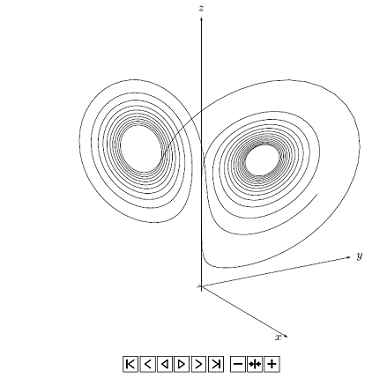
Diese Darstellung des Lorenz-Attraktors verwendet Mit Die Achsen habe ich verborgen, um erstmal das pure Bild zu erhalten, dennoch wären dezente Achsen und evtl. ein Grid unten in der xy-Ebene eine Unterstützung des dreidimensionalen Eindrucks, die voreingestellten Achsen waren mir nur zu wuchtig (einfach \documentclass[border=10pt]{standalone} \usepackage{pgfplots} \pgfplotsset{compat=1.8} \begin{document} \begin{tikzpicture} \begin{axis}[ xmin = -25, xmax = 25, ymin = -25, ymax = 25, zmin = 0, zmax = 50, hide axis, ] \addplot3[mark=none, mesh, shader=interp, color=black, opacity=0.2] file { lorenz.dat }; \end{axis} \end{tikzpicture} \end{document}
|
|
Eine Lösung, die mit LuaTeX die Differentialgleichung löst. (Ganz frech abgeschrieben aus Juan Montijano, Mario Pérez, Luis Rández and Juan Luis Varona. "Numerical methods with LuaLaTeX". TUGboat 35:1, 2014, frei verfügbar im PracTeX Journal) \documentclass[tikz]{standalone} \usepackage{luacode,pgfplots} \begin{luacode*} -- Differential equation of Lorenz attractor function f(x,y,z) local sigma = 3 local rho = 26.5 local beta = 1 return {sigma*(y-x),-x*z + rho*x - y,x*y - beta*z} end -- Code to write PGFplots data as coordinates function print_LorAttrWithEulerMethod(h,npoints,option) -- The initial point (x0,y0,z0) local x0 = 0.0 local y0 = 1.0 local z0 = 0.0 -- add random number between -0.25 and 0.25 local x = x0 + (math.random()-0.5)/2 local y = y0 + (math.random()-0.5)/2 local z = z0 + (math.random()-0.5)/2 if option ~= [[]] then tex.sprint("\\addplot3[" .. option .. "] coordinates{") else tex.sprint("\\addplot3 coordinates{") end -- dismiss the first 100 points -- to go into the attractor for i=1, 100 do m = f(x,y,z) x = x + h * m[1] y = y + h * m[2] z = z + h * m[3] end for i=1, npoints do m = f(x,y,z) x = x + h * m[1] y = y + h * m[2] z = z + h * m[3] tex.sprint("("..x..","..y..","..z..")") end tex.sprint("}") end \end{luacode*} \newcommand\addLUADEDplot[3][]{% \directlua{print_LorAttrWithEulerMethod(#2,#3,[[#1]])}% } \pgfplotsset{width=.9\hsize} \begin{document} \begin{tikzpicture} \begin{axis} % SYNTAX: Solution of the Lorenz system % with step h=0.02 sampled at 1000 points. \addLUADEDplot[color=red,smooth]{0.02}{1000}; \addLUADEDplot[color=green,smooth]{0.02}{1000}; \addLUADEDplot[color=blue,smooth]{0.02}{1000}; \addLUADEDplot[color=cyan,smooth]{0.02}{1000}; \addLUADEDplot[color=magenta,smooth]{0.02}{1000}; \addLUADEDplot[color=yellow,smooth]{0.02}{1000}; \end{axis} \end{tikzpicture} \end{document} Schöne Farben, aber es sind 6 nebeneinanderliegende Attraktoren mit geringfügig variierten Anfangsbedingungen. Interessanter wäre es, wenn sich die Farbe entlang der Trajektorie eines einzigen Attraktors ändern würde. Mir fällt aber gerade kein geeignetes Kriterium ein. Vielleicht der Biegeradius? Ach ja, Euler ist nur ein Verfahren 1. Ordnung, aber das spielt ja keine Rolle hier. ;)
(29 Jun '14, 19:54)
AlexG
|
|
Eine weitere "Animation" eines Lorenz-Attraktors mit dem Ein-faches Kompilieren mit
% arara: latex % arara: latex % arara: dvips % arara: ps2pdf %%% A C H T U N G - 'kann' ein Weilchen dauern! %%% \documentclass{article} \usepackage{multido} \usepackage{pst-3dplot} \usepackage{pst-ode} \usepackage{animate} \begin{document} %Lorenz’ set of differential equations \def\lorenz{% 10*(x[1]-x[0]) | %dx/dt x[0]*(28-x[2]) - x[1] | %dy/dt x[0]*x[1] - 8/3*x[2] %dz/dt }% % %write timeline file \newwrite\OutFile% \immediate\openout\OutFile=lorenz.tln% \multido{\iLorenz=0+1}{101}{% \immediate\write\OutFile{::\iLorenz x0}% }% \immediate\write\OutFile{::c,101}% \multido{\iLorenz=102+1}{89}{% \immediate\write\OutFile{::\iLorenz}% }% \immediate\closeout\OutFile% % \psset{unit=0.155,linewidth=0.5pt}% \begin{animateinline}[ timeline=lorenz.tln, controls,poster=last, begin={\begin{pspicture}(-39,-13)(39,60)}, end={\end{pspicture}} ]{10} %coordinate axes \psset{Alpha=120,Beta=20}% \pstThreeDCoor[xMax=33,yMax=33,zMax=55,linecolor=black]% \newframe \pstODEsetOrRestoreState{10 10 30} %initial condition \multiframe{100}{i=0+1,rtZero=0+0.25,rtOne=0.25+0.25}{% \pstODEsaveState{savedState}% %compute attractor segments, stored in ‘lorenzXYZseg’ \pstODEsolve[algebraic]{lorenzXYZseg}{0 1 2}{\rtZero}{\rtOne}{26}{savedState}% {\lorenz}% %compute the whole attractor, stored in ‘lorenzXYZall’, with the same stepping \ifnum\i=0\relax% \pstODEsolve[algebraic]{lorenzXYZall}{0 1 2}{\rtZero}{\rtOne}{26}{savedState}% {\lorenz}% \else% \pstODEsolve[algebraic,append]{lorenzXYZall}{0 1 2}{\rtZero}{\rtOne}{26}% {savedState}{\lorenz}% \fi% \listplotThreeD[plotstyle=line]{lorenzXYZseg}% }% \newframe% required between two \multiframe \multiframe{90}{rAlpha=116+-4}{% fly-around \psset{Alpha=\rAlpha,Beta=20}% \pstThreeDCoor[xMax=33,yMax=33,zMax=55,linecolor=black]% \listplotThreeD[plotstyle=line]{lorenzXYZall}% }% \end{animateinline} \end{document} Das braucht bei der ersten Erstellung zwei
(01 Jul '14, 12:56)
esdd
Bei mir ging das einfach so, aber, wie gesagt, nur im AdobeReader. Ich hab es einfach mal ergänzt, schaden kann es ja auch nicht. Und in Sumatra war ich noch nie ;)
(01 Jul '14, 13:03)
cis
|