|
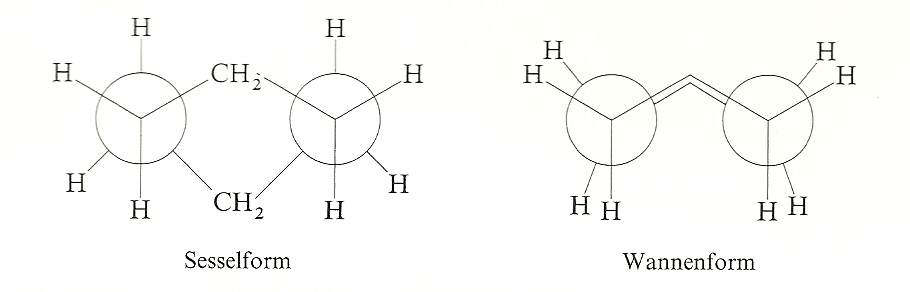
Ich hätte gern einen cyclohexanring in Newman-Projektion dargestellt wie im Bild. Weiß vllt. jmd. wie man das z.B. mit dem newman-Befehl aus dem chemmacros-paket hinbekommt ?
|
|
Die Sessel-Konformation lässt sich mit wenig Aufwand tatsächlich mit Die erste Variante ist einfach: zweimal \newman{H,H,,H,,H}\hspace*{-4pt}\newman{H,,H,H,H} Bei der zweiten muss man ein bisschen tricksen: für die Methylen-Gruppen ein \newman{H,H,C\rlap{\ch{H2}},H,C\rlap{\ch{H2}},H}\hspace*{10pt}\newman{H,,H,H,H} So sieht's dann aus:
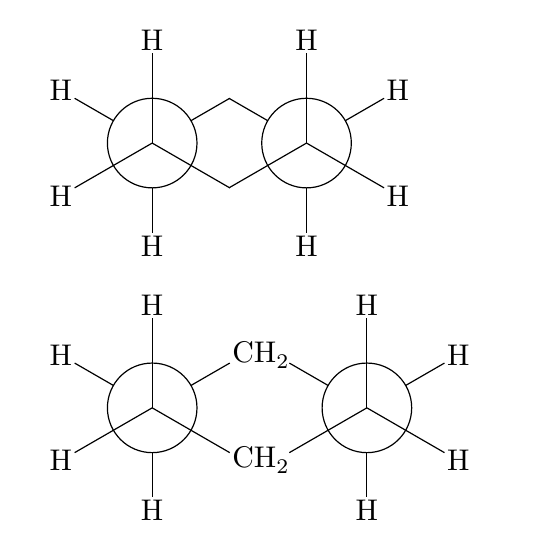
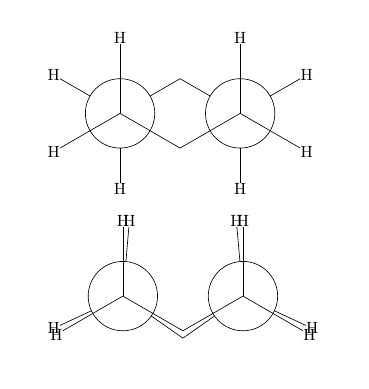
\documentclass{article} \usepackage{chemmacros} \begin{document} \newman{H,H,,H,,H}\hspace*{-4pt}\newman{H,,H,H,H} \bigskip \newman{H,H,C\rlap{\ch{H2}},H,C\rlap{\ch{H2}},H}\hspace*{10pt}\newman{H,,H,H,H} \end{document} Die Wannen-Konformation ist mit Mit TikZ lässt sie sich natürlich ohne weiteres zeichnen. Wenn man dann schon dabei ist, kann man die Sessel-Konformation dann ebenfalls mit TikZ zeichnen. Das folgende ist eine nicht sehr automatisierte Variante, sondern das erstbeste, was mir eingefallen ist, ohne ins TikZ-Handbuch zu schauen. Das erste \documentclass{article} \usepackage{tikz} \usetikzlibrary{calc,intersections} \begin{document} \begin{tikzpicture} % die beiden Haupt-C-C-Achsen als Koordinaten definieren, % als Bindungslänge habe ich 1.5 ausgewählt: \coordinate (C1) at (0,0) ; \coordinate (C2) at ($cos(30)*(3,0)$) ; % benötigt `calc'-Bibliothek, % cos(30) ergibt sich aus einfacher Geometrie % Koordinaten in entsprechendem Abstand und Winkel von den Zentren definieren % und die vorderen Bindungen malen: \foreach \angle in {90,210,330} { \draw (C1) -- ++(\angle:1.5) coordinate (C1-\angle) ; \draw (C2) -- ++(\angle:1.5) coordinate (C2-\angle) ; } % die Kreise malen: \draw (C1) circle (.75) (C2) circle (.75) ; % die hinteren Bindungen malen und ebenfalls Koordinaten an deren Enden definieren: \foreach \angle in {30,150,270} { \draw (C1) ++(\angle:.75)--++(\angle:.75) coordinate (C1-\angle) ; \draw (C2) ++(\angle:.75)--++(\angle:.75) coordinate (C2-\angle) ; } % an den äußeren Bindungen H-Atome platzieren: \foreach \angle in {90,150,210,270} { \node[inner sep=0,anchor=180+\angle] at (C1-\angle) {H} ; } \foreach \angle in {30,90,270,330} { \node[inner sep=0,anchor=180+\angle] at (C2-\angle) {H} ; } \end{tikzpicture} \bigskip \begin{tikzpicture} \coordinate (C1) at (0,0) ; \coordinate (C2) at ($cos(30)*(3,0)$) ; \foreach \angle in {90,210,330} { \draw (C1) -- ++(\angle:1.5) coordinate (C1-\angle) ; \draw (C2) -- ++(\angle:1.5) coordinate (C2-\angle) ; } \draw (C1) circle (.75) (C2) circle (.75) ; \foreach \angle in {85,205} { \draw (C1) ++(\angle:.75)--++(\angle:.75) coordinate (C1-\angle) ; } \foreach \angle in {95,335} { \draw (C2) ++(\angle:.75)--++(\angle:.75) coordinate (C2-\angle) ; } \path [name path=C1] (C1) --++(325:2) ; \path [name path=C2] (C2) --++(215:2) ; \draw [name intersections={of=C1 and C2}] (C1) ++(325:.75) -- (intersection-1) (C2) ++(215:.75) -- (intersection-1) ; \foreach \angle in {85,90,205,210} { \node[inner sep=0,anchor=180+\angle] at (C1-\angle) {H} ; } \foreach \angle in {90,95,330,335} { \node[inner sep=0,anchor=180+\angle] at (C2-\angle) {H} ; } \end{tikzpicture} \end{document}
Abgesehen vielleicht von der @clemens also die Lösung per tikz würde mich auch interessieren - dann auch im hinblick auf die wannenform! soll ich die Frage dann nochmal stellen mit der Vorgabe tikz statt chemmacros zu verwenden?
(12 Jul '14, 21:20)
butts
@butts Ich hab eine TikZ-Version hinzugefügt. Das meiste was ich verwendet habe, ist Basis-TikZ (darüber hinaus bin ich nie gekommen). Du solltest mal in das TikZ-Handbuch schauen und Dir die Beispiele zu Gemüte führen. Es enthält ganz exzellente Tutorials und danach kannst Du sowas selbst.
(12 Jul '14, 22:42)
cgnieder
|