|
Ich wollte mit pgf/TikZ einen Funktionsgraphen zeichnen und habe dafür zunächst das Bild mit Geogebra erstellt und dann als TikZ-Code exportiert. Das Bild sieht ähnlich zum folgenden aus: Compilieren des Codes ergab die Fehlermeldung ! Package PGF Math Error: Unknown function `x' (in '{x^2*sin((1/(0.01))*180/pi)}'). Mein Beispielcode: \documentclass[book,12pt,titlepage]{scrartcl} \usepackage[T1]{fontenc} \usepackage{ngerman} \usepackage[latin1]{inputenc} \usepackage{pdfpages} \usepackage{pgf,tikz} \usetikzlibrary{shapes,shadows,arrows,intersections,matrix} \usetikzlibrary{decorations.pathmorphing} \usetikzlibrary{decorations.markings} \begin{document} \definecolor{cczzqq}{rgb}{0.8,0.6,0} \definecolor{qqzzcc}{rgb}{0,0.6,0.8} \begin{tikzpicture}[line cap=round,line join=round,>=triangle 45,x=1.0cm,y=1.0cm] \draw[->,color=black] (-0.5,0) -- (0.5,0); \foreach \x in {-0.5,-0.4,-0.3,-0.2,-0.1,0.2,0.3,0.4} \draw[shift={(\x,0)},color=black] (0pt,2pt) -- (0pt,-2pt) node[below] {\footnotesize $\x$}; \draw[->,color=black] (0,-0.26) -- (0,0.52); \foreach \y in {-0.2,0.2,0.3,0.4,0.5} \draw[shift={(0,\y)},color=black] (2pt,0pt) -- (-2pt,0pt) node[left] {\footnotesize $\y$}; \draw[color=black] (0pt,-10pt) node[right] {\footnotesize $0$}; \clip(-0.5,-0.26) rectangle (0.5,0.52); \draw[smooth,samples=100,domain=0.01:0.4957841792409696] plot(\x,{x²*sin((1/(\x))*180/pi)}); \draw[smooth,samples=100,domain=-0.5:0.01] plot(\x,{x²*sin((1/(\x))*180/pi)}); \draw[color=qqzzcc, smooth,samples=100,domain=-0.5015272062185642:0.4957841792409696] plot(\x,{0-x²}); \draw[color=cczzqq, smooth,samples=100,domain=-0.5015272062185642:0.4957841792409696] plot(\x,{x²}); \draw[color=cczzqq, smooth,samples=100,domain=-0.5015272062185642:0.4957841792409696] plot(\x,{x²}); \draw (-0.27,0.18) node[anchor=north west] {$y=x^2\cdot \sin ( 1/x)$}; \end{tikzpicture} \end{document} Was an der pgf-Funktionsdefinition ist denn falsch ?
Ergebnis 5 von 10
show 5 more comments
|
|
Der von geogebra exportierte Code ist leider fehlerhaft. Für das Plotten von Funktionen bietet sich das Paket |
|
Eine geogebra-Übersetzung darf man sich am Anfang schon mal ausgeben lassen. Allerdings sollte man sich, den Code betrachtend, fragen:
Wenn man das, neben dem bereits genannten Eingabefehler, alles mal der Reihe nach korrigiert, dann klappt das auch:
\documentclass[margin=2.5mm]{standalone} \usepackage[ngerman]{babel} \usepackage{tikz} \usepackage{amsmath, amssymb} %=========== \begin{document} %=========== \begin{tikzpicture}[x = 52.5cm, y=150.5cm, scale=0.25, font=\footnotesize, >=latex %Voreinstellung für Pfeilspitzen ] % Gitternetzlinien %\draw[ help lines] (-3.5,-3.5) grid (3.5,3.5); % x-Achse \draw[->] (-0.55,0) -- (0.55,0) node[below] {$x$}; %Zahlen auf x-Achse \foreach \x in {-0.5,-0.25,0.25,0.5} \draw[shift={(\x,0)},color=black] (0pt,2pt) -- (0pt,-2pt) node[below] {$\x$}; % y-Achse \draw[->] (0,-0.12) -- (0,0.12) node[left] {$y$}; %Zahlen auf y-Achse \foreach \y in {-0.1,-0.05,0.05,0.1} \draw[] (2pt,\y) -- (-2pt,\y) node[left] {$\y$}; %Ursprung \draw[color=black] (0pt,-5pt) node[right] {$0$}; %%%%%%%%%%%%%%%% %% FUNKTION %% %%%%%%%%%%%%%%%% \draw[thick,red] plot[samples=800, domain=0.01:0.4] (\x,{((\x)^2)*sin((1/\x) r)}) node[above, right] {$f(x)=x^2 \cdot \sin\left(\frac{1}{x}\right)$}; \draw[thick,red] plot[samples=600, domain=-0.01:-0.4] (\x,{((\x)^2)*sin((1/\x) r)}); %Einhüllende \draw[densely dashed] plot[domain=-0.3:0.3](\x,{(\x)^2}); % \draw[densely dashed] plot[domain=-0.3:0.3](\x,{-(\x)^2}); \end{tikzpicture} %=========== \end{document} %=========== |

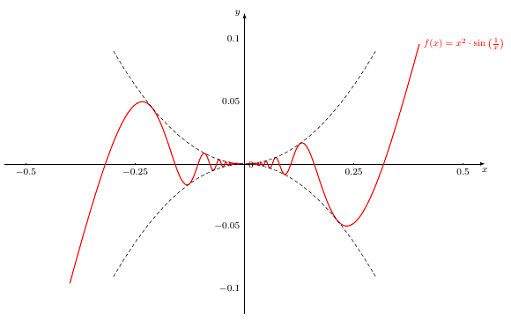
Wenn Du Dir in Deinem Code den betreffenden Teil genau anschaust, dann siehst Du ein
x²wo ein\x^2sein sollte. Das taucht mindestens fünfmal auf, wenn ich mich nicht verzählt habe.Der Export aus Geogebra ist nicht optimal. Schau dir allein die verschiedenen Domaingrenzen an.
@butt der Fehler taucht auf, wenn TeX mit zu großen Zahlen rechnen muss, siehe Origin and formation to the ERROR ‘Dimension too large’
Ich habe den Kommentar mit der neuen Fehlermeldung in eine neue Frage umgewandelt. Bitte Folgefragen neu formulieren, denn nur in Kommentaren kann man keine Lösungen präsentieren und die Übersicht geht verloren. Die neue Frage kannst Du editieren, optimalerweise den verursachenden Code einfügen, hier: ! Dimension too large mit pgfplots, wie behebe ich den Fehler?
Vielleicht lädst du mal ein Bild hier hoch, damit man einen Eindruck von dem gewünschten Ergebnis bekommt. Ich bin sicher, dass man das dann mit halb so viel handgeschriebenem Code nachbauen kann.
@Clemens eine der Antworten in dem von Dir verlinkten Beitrag des englischsprachigen Forums lautet: TeX dimen arithmetic is not floating point: it is fixed point, basically it just does 30 bit (+sign bit) integer arithmetic in sp units.
Also da steige ich aus - das verstehe ich gar nicht! :-(
Es scheint ein Problem mit der Größe des Definitionsbereichs der Funktion zu sein, die gezeichnet werden soll.
wenn ich den numerischen Wert von x^2(sin(1/x)) mal ausrechne dann ergibt sich für x= 0.01 : 8.26 x 10^{-5} und für x=0,49 : 0.2140
Also das sind doch jetzt keine übergroßen Zahlen ???
Pgfplots rechnet intern ein wenig anders. Das reziproke sehr kleiner Zahlen sind sehr große Zahlen. Kann sein, dass die Transformation etwas Unendliches ausspuckt.
@Johannes ... ja aber das ist doch stets so ! der Kehrwert sehr kleiner Zahlen ergibt sehr große Zahlen. DAS ist doch kein Spezifikum einer Programmiersprache o.ä. ! Was meinst Du denn mit TRANSFORMATION ? Unter dem Begriff kann ich mir garnichts vorstellen . Meinst Du damit vllt. die Rechenvorgänge die intern beim compilieren ablaufen ?
Schau einfach mal in die Dokumentation von pgfplots. Da steht auch drin, wieso der Fehler kommt (kommen könnte) undmögliche Lösungen werden auch gegeben.
@all Die Frage hier ist über den Fehler "Unknown function `x'" und dieses x²-Problem. Bitte nicht an dieser Stelle über sich anschließend ergebende Probleme diskutieren, sonst haben wir einen unübersichtlichen Wust an Kommentaren, die man nicht taggen kann und keine Lösungen markieren etc. Oben habe ich zu der Folgefrage verlinkt, in die ich butts' Kommentarfrage konvertiert habe. (Auch wenn es eng zusammenhängt und das Eingangsproblem vllt. für sich stehend nicht grad das Nachwelt-wichtigste ist, Prinzip- und Ordnungsfrage)