|
Hallo, die folgende Frage wurde bereits im golatex-Forum gepostet, wo man mich hierher verwies. Ich möchte die Anisotropie eines Einkristalls mittels des E-Moduls im dreidimensionalen Raum in Abhängigkeit der Kristallrichtungen darstellen. Dazu soll zunächst die Elastizitätsmatrix von Silizium genutzt werden: Elastischen Konstanten: Diese Konstanten gelten für ein parallel zu den
Zur Umsetzung bin ich auf das Paket Nun ist jedoch die Frage, wie ich meine Elastizitätsmatrix hier implementiere und diese dann auch zum Rotieren um den Koordinatenursprung bringe. Kann hier jemand einen Tip geben bzw. gibt es alternative Lösungsmöglichkeiten?
Zur Formel... Komponenten der Steifigkeitstetrade bezogen auf eine Orthonormalbasis: Eine Rotation des Koordinatensystems mit einem Winkel Einsteinsche Summenkonvention gilt, In Mathematica hat es schon einmal jemand umgesetzt. Ein Code-Beispiel gibt es dort auch: Anisotropic Elasticity Ich habe es mal nachgebastelt: Seite 1 Seite 2 Vielleicht wird die Mathematik hierbei klarer. Eine exemplarische Plot-Funktion sollte lauten:
Ergebnis 5 von 7
show 2 more comments
|
|
Wenn du die richtige Formel gefunden hast, ist der Rest recht einfach: Du ersetzt alle Mir scheint, dass
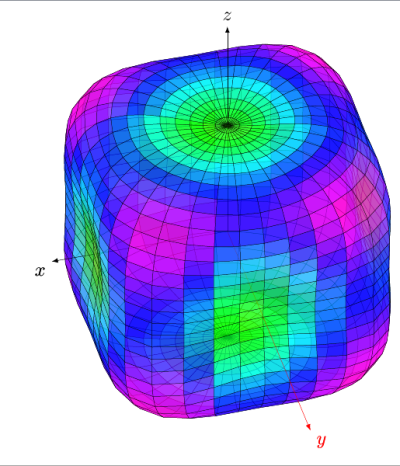
die richtige Formel ist. Mit dieser Formel und dem Code unten erhalte ich folgendes Bild.
Danke für die Antwort! An dieser Stelle möchte ich noch eine Frage nachschieben. Welche Möglichkeiten der Farbdarstellungen gibt es für diesen Plot? Sind monochromatische Farbabstufungen möglich?
(14 Nov '14, 20:02)
Dirk
3
@Dirk kannst du die Frage extra posten? Ich denke das wäre auch unabhängig von der Eingangsfrage interessant.
(15 Nov '14, 16:55)
sudo
Hier gehts weiter: Farbdarstellungsmöglichkeiten mit tikz-3dplot
(16 Nov '14, 18:21)
Dirk
|


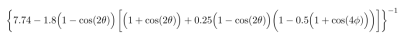
Ich meinte eigentlich eher eine Formel der Form
$f(x,y,z)=\ldots$.AFAIK ist es am besten, wenn du die Formel noch von Kugelkoordinaten in Kartesische Koordinaten umrechnest.
Wie Du in dem oberen Beispiel siehst, kann tikz-3dplot auch mit Polarkoordinaten umgehen. Es sollte also möglich sein, r in Abhängigkeit von phi und theta zu plotten. Eigentlich wollte ich die Eingabe nicht einmal auf die oben angegebene, exemplarische Plot-Funktion herunter brechen.
@Dirk Sorry, du hast recht mit den Kugelkoordinaten, aber deine Formel scheint nicht zu stimmen. Das Ergebnis stimmt nicht mit deiner Graphik überein.
Oh Mann, immer wenn man denkt, man hätte alles gesehen... :)
Ich habe die Frage wieder geöffnet. Das Schließen hat eigentlich den Sinn, Fragen, die doppelt gestellt sind (Duplikate) zusammenzuführen, Offtopic-Fragen „abzuwehren“ etc. Dass die Frage beantwortet wurde und die Antwort akzeptiert wurde, sieht man auch so. Wenn man die Frage aber schließt, verhindert man aber auch, dass irgendwann in der Zukunft vielleicht noch jemand mit einer Alternative antworten kann... daher ist es besser, diese Frage offen (was nicht das gleiche wie unbeantwortet ist) zu lassen.
ODer vielleicht besser gesagt, offen für Alternativvorschläge. Denn die Frage an sich scheint ja beantwortet.