|
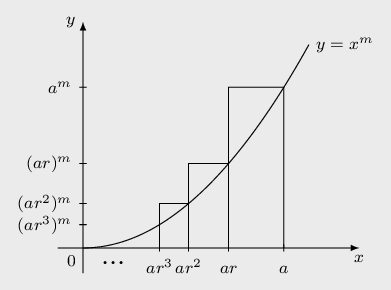
Hallo! Ich habe kürzlich einen Graphen mit TikZ erstellt (es geht hier um die sogen. "Fermatsche Integration"). Nun geht mir TikZ recht leicht von der Hand, mit pgfplots tue ich mich noch schwer, etwa wegen den teils schon unterschiedlichen Notationen und, um es nicht zu vergessen, mir in Details zu viele Vorgaben gemacht werden (z.B. Pfeilspitzen oder sowas). Wobei das Paket pgfplots schon eine beachtliche Leistung ist (siehe z.B. das ternary diagram) und mir auffällt, daß sich dort der Code ggü. Tikz oft drastisch verkürzt. Meine Frage ist ist also eher allgemeiner Natur, ich weiß nicht, ob sie sich beantworten läßt. Wäre z.B. bei diesem Graphen pgfplots sinnvoller gewesen? Danke! \documentclass[varwidth, margin=5pt]{standalone} \usepackage[ngerman]{babel} \usepackage{tikz} \usetikzlibrary{calc} \usepackage{amsmath, amssymb} \pagecolor{lightgray!40} %=========== \begin{document} %=========== \def\r{0.725} \def\a{4} \begin{tikzpicture}[font=\footnotesize, >=latex, scale=0.85] %KoSy %\draw[very thin,color=gray] (-2,-4) grid (3,4); \draw[->] (-0.5,0) -- (5.5,0) node[right, below] {$x$}; \draw[->] (0,-0.5) -- (0,4.5) node[above, left] {$y$}; %Achsenbeschriftung %Ursprung \node[below left] {$0$}; % ---------------- \coordinate (Nx) at (\a,0); \coordinate (Ny0) at ($({0},{0.2*\a^2})$); \coordinate (Ny) at ($({\a},{0.2*\a^2})$); \coordinate (Mx) at ($({\a*\r},{0})$); \coordinate (My0) at ($({0},{0.2*(\a*\r)^2})$); \coordinate (My1) at ($({\a*\r},{0.2*(\a)^2})$); \coordinate (My) at ($({\a*\r},{0.2*(\a*\r)^2})$); \coordinate (Lx) at ($({\a*\r^2},{0})$); \coordinate (Ly0) at ($({0},{0.2*(\a*\r^2)^2})$); \coordinate (Ly1) at ($({\a*\r^2},{0.2*(\a*\r)^2})$); \coordinate (Ly) at ($({\a*\r^2},{0.2*(\a*\r^2)^2})$); \coordinate (Kx) at ($({\a*\r^3},{0})$); \coordinate (Ky0) at ($({0},{0.2*(\a*\r^3)^2})$); \coordinate (Ky1) at ($({\a*\r^3},{0.2*(\a*\r^2)^2})$); \coordinate (Ky) at ($({\a*\r^3},{0.2*(\a*\r^3)^3})$); % ---------------- %x-Achse: \draw[] ([yshift=2pt]Nx.north)--([yshift=-2pt]Nx.south) node[below]{$a \vphantom{ar^2}$}; \draw[] ([yshift=2pt]Mx.north)--([yshift=-2pt]Mx.south) node[below]{$ar\vphantom{ar^2}$}; \draw[] ([yshift=2pt]Lx.north)--([yshift=-2pt]Lx.south) node[below]{$ar^2$}; \draw[] ([yshift=2pt]Kx.north)--([yshift=-2pt]Kx.south) node[below]{$ar^3$}; \node[] at ([xshift=-15mm, yshift=-3mm]Lx.south west) {\Large$...$}; %y-Achse: \draw[] ([xshift=2pt]Ny0.east)--([xshift=-2pt]Ny0.west) node[left]{$a^m$}; \draw[] ([xshift=2pt]My0.east)--([xshift=-2pt]My0.west) node[left]{$(ar)^m$}; \draw[] ([xshift=2pt]Ly0.east)--([xshift=-2pt]Ly0.west) node[left]{$(ar^2)^m$}; \draw[] ([xshift=2pt]Ky0.east)--([xshift=-2pt]Ky0.west) node[left]{$(ar^3)^m$}; %Rechtecke \draw[thin] (Nx) -- (Ny) -- (My1) -- (Mx); \draw[thin] (My) -- (Ly1) -- (Lx); \draw[thin] (Ly) -- (Ky1) -- (Kx); %Kurve \draw[] plot[domain=0:4.5, samples=400,] (\x,{0.2*\x^2}) node[right] {$y=x^m$}; \end{tikzpicture} %=========== \end{document} %=========== |
|
Zu pgfplots würde ich wechseln, wenn z.B. einer der Punkte zutrifft:
Das hier gezeigte Beispiel ist natürlich ein ganz einfaches, wo man mit pgfplots noch nicht viel gewinnen oder einsparen kann. Wenn man sowieso komplexere Plots haben könnte, lohnt sich die Einarbeitung in pgfplots, und dann sind auch die einfachen Plots damit Routinesache und konsistent im Aussehen zu den komplexeren. Einen Eindruck von den Fähigkeiten bieten neben dem Handbuch z.B. die PGFPlots-Galerie und auch die TeXwelt-Beispiele. Bei Plots will ich gar nicht mehr auf pgfplots verzichten. Mit TikZ ergänzend etwas einzeichnen geht immer noch. |

Pgfplots ist vor allem dafür konzipiert, aus Messwerten Diagramme zu erstellen. Wenn um das Plotten von Funktionen und ggf. das Einfügen irgendwelcher Annotations geht, dann ist TikZ (besonders seit 3.0) imho besser geeignet.